
【题目】已知函数![]() (
(![]() 且
且![]() ).
).
(1)讨论函数![]() 的单调性;
的单调性;
(2)若![]() ,讨论函数
,讨论函数![]() 在区间
在区间![]() 上的最值.
上的最值.
【答案】(1)见解析;(2)见解析.
【解析】
(1)求出![]() ,分三种情况讨论
,分三种情况讨论![]() 的范围,在定义域内,分别由
的范围,在定义域内,分别由![]() 求出
求出![]() 的范围,可得增区间;由
的范围,可得增区间;由![]() 求出
求出![]() 的范围, 可得减区间;(2)由(1)得,当
的范围, 可得减区间;(2)由(1)得,当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,分四种情况讨论,分别利用导数判断函数在
上单调递增,分四种情况讨论,分别利用导数判断函数在![]() 上的单调性,利用单调性求出极值,与
上的单调性,利用单调性求出极值,与![]() 的值比较大小,进而可得结果.
的值比较大小,进而可得结果.
(1)函数![]() 的定义域是
的定义域是![]() .
.
![]() .
.
当![]() 时,令
时,令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() ,
,
所以函数![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减;
上单调递减;
当![]() 时,令
时,令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() ,
,
所以函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增.
上单调递增.
(2)由(1)得,当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增.
上单调递增.
①当![]() ,即
,即![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递减,所以函数
上单调递减,所以函数![]() 在
在![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为![]() ;
;
②当![]() ,即
,即![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递增,所以函数
上单调递增,所以函数![]() 在
在![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为![]() ;
;
③当![]() ,即
,即![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,所以函数
上单调递增,所以函数![]() 在
在![]() 上的最小值为
上的最小值为![]() .
.
最大值为![]() 与
与![]() 中的较大者.下面比较
中的较大者.下面比较![]() 与
与![]() 的大小:
的大小:
因为![]()
![]() ,
,
令![]() ,得
,得![]() ,化简得
,化简得![]() ,
,
解得![]()
![]() .因为
.因为![]() ,且
,且![]() ,
,
所以![]() .
.
所以当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上的最大值为
上的最大值为![]() ;
;
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上的最大值为
上的最大值为![]() ;
;
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上的最大值为
上的最大值为![]() .
.
综上,当![]() 时,函数
时,函数![]() 在
在![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为![]() ;
;
当![]() 时,函数
时,函数![]() 在
在![]() 上的最大值为
上的最大值为![]() ;最小值为
;最小值为![]() ;
;
当![]() 时,函数
时,函数![]() 在
在![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为![]() ;
;
当![]() 时,函数
时,函数![]() 在
在![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为![]() .
.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:
【题目】进入![]() 月份,香港大学自主招生开始报名,“五校联盟”统一对五校高三学生进行综合素质测试,在所有参加测试的学生中随机抽取了部分学生的成绩,得到如图所示的成绩频率分布直方图:
月份,香港大学自主招生开始报名,“五校联盟”统一对五校高三学生进行综合素质测试,在所有参加测试的学生中随机抽取了部分学生的成绩,得到如图所示的成绩频率分布直方图:
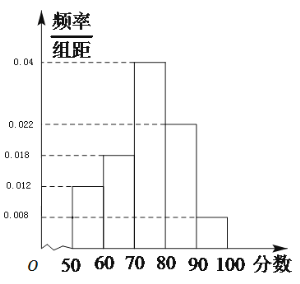
(1)估计五校学生综合素质成绩的平均值;
(2)某校决定从本校综合素质成绩排名前![]() 名同学中,推荐
名同学中,推荐![]() 人参加自主招生考试,若已知
人参加自主招生考试,若已知![]() 名同学中有
名同学中有![]() 名理科生,2名文科生,试求这3人中含文科生的概率.
名理科生,2名文科生,试求这3人中含文科生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个圆经过点![]() ,且和直线
,且和直线![]() 相切.
相切.
(1)求动圆圆心的轨迹![]() 的方程;
的方程;
(2)已知点![]() ,设不垂直于
,设不垂直于![]() 轴的直线
轴的直线![]() 与轨迹
与轨迹![]() 交于不同的两点
交于不同的两点![]() ,若
,若![]() 轴是
轴是![]() 的角平分线,证明直线
的角平分线,证明直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】篮球运动于1891年起源于美国,它是由美国马萨诸塞州斯普林菲尔德(旧译麻省春田)市基督教青年会(![]() )训练学校的体育教师詹姆士·奈史密斯博士(
)训练学校的体育教师詹姆士·奈史密斯博士(![]() )发明.它是以投篮、上篮和扣篮为中心的对抗性体育运动之一,是可以增强体质的一种运动.已知篮球的比赛中,得分规则如下:3分线外侧投入可得3分,3分线内侧投入可得2分,不进得0分.经过多次试验,某人投篮100次,有20个是3分线外侧投入,30个是3分线内侧投入,其余不能入篮,且每次投篮为相互独立事件.
)发明.它是以投篮、上篮和扣篮为中心的对抗性体育运动之一,是可以增强体质的一种运动.已知篮球的比赛中,得分规则如下:3分线外侧投入可得3分,3分线内侧投入可得2分,不进得0分.经过多次试验,某人投篮100次,有20个是3分线外侧投入,30个是3分线内侧投入,其余不能入篮,且每次投篮为相互独立事件.
(1)求该人在4次投篮中恰有三次是3分线外侧投入的概率;
(2)求该人在4次投篮中至少有一次是3分线外侧投入的概率;
(3)求该人两次投篮后得分![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为调研学校师生的环境保护意识,决定在本市所有学校中随机抽取60所进行环境综合考评成绩达到80分以上(含80分)为达标.60所学校的考评结果频率分布直方图如图所示(其分组区间为[50,60),[60,70),[70,80),[80,90),[90,100]).

(Ⅰ)试根据样本估汁全市学校环境综合考评的达标率;
(Ⅱ)若考评成绩在[90.100]内为优秀.且甲乙两所学校考评结果均为优秀从考评结果为优秀的学校中随机地抽取两所学校作经验交流报告,求甲乙两所学校至少有一所被选中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com