练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某特色餐馆开通了美团外卖服务，在一周内的某特色菜外卖份数（份）与收入（元）之间有如下的对应数据：

    外卖份数（份）

    2

    4

    5

    6

    8

    收入（元）

    30

    40

    60

    50

    70

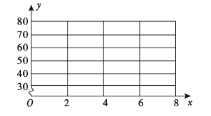
    （1）画出散点图；

    （2）求回归直线方程；

    （3）据此估计外卖份数为12份时，收入为多少元．

    注：①参考公式：线性回归方程系数公式， ；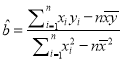

    ②参考数据： ， ， ．

    【答案】（1）见解析（2）；（3）95.5元．

    【解析】试题分析：(1)根据表中数据,作出散点图即可;
    (2)计算、,求出回归系数,写出回归直线方程;
    (3)由回归直线方程,计算x=12时的值即可.

    试题解析： （1）作出散点图如下图所示：

    （2），

    ，

    已知， ．

    由公式， ，可求得， ，

    因此回归直线方程为；

    （3）时， ．

    即外卖份数为12份时，收入大约为95.5元．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知等差数列{an}中，a1=1，且a2+2，a3 ， a4﹣2成等比数列．
    （1）求数列{an}的通项公式；
    （2）若bn= ，求数列{bn}的前n项和Sn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四棱锥P﹣ABCD中，底面ABCD为直角梯形，AD∥BC，AB⊥BC侧面PAB⊥底面ABCD，PA=AD=AB=2，BC=4．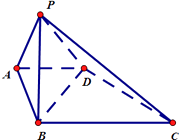

    （1）若PB中点为E．求证：AE∥平面PCD；
    （2）若∠PAB=60°，求直线BD与平面PCD所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出下列命题：

    ① “若，则有实根”的逆否命题为真命题；

    ②命题“”为真命题的一个充分不必要条件是；

    ③命题“，使得”的否定是真命题；

    ④命题函数为偶函数，命题函数在上为增函数，

    则为真命题.

    其中，正确的命题是（ ）

    A. ①② B. ①③ C. ②③ D. ③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】等比数列{an}的各项均为正数，且2a1+3a2=1，a32=9a2a6 ．
    （1）求数列{an}的通项公式；
    （2）设bn=|10+2log3an|，求数列{bn}的前n项和Sn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列说法中正确的是（ ）
    A.数据4、6、6、7、9、4的众数是4
    B.一组数据的标准差是这组数据的方差的平方
    C.数据3，5，7，9的标准差是数据6、10、14、18的标准差的一半
    D.频率分布直方图中各小长方形的面积等于相应各组的频数

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知sin（π﹣α）﹣cos（π+α）= （ ＜α＜π）．求：
    （1）sinα﹣cosα；
    （2）tanα+ ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= 的定义域为A．
    （1）求A；
    （2）已知k＞0，集合B={x| }，且A∩B≠，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，三棱柱中，已知侧面， ， ， .

    （1）求证： 平面；

    （2）是棱上的一点，若二面角的正弦值为，求线段的长.

    查看答案和解析>>

    同步练习册答案