【题目】已知函数 
的最小正周期为π．
（1）求 
的值；
（2）求函数f（x）的单调递增区间及其图象的对称轴方程．
【答案】
（1）解： 
= 
，
因为f（x）最小正周期为π，所以 
，解得ω=1，
所以 
，
所以 
．
（2）解：由 
，
得 
，
所以，函数f（x）的单调增区间为 
；
由 
得 
，
所以，f（x）图象的对称轴方程为 ．
【解析】（1）利用两角差的正弦公式的应用，化简f（x）的解析式，和周期，即可求出ω，把 
代入函数解析式即可求得结果；（2）根据正弦曲线的对称轴，写出函数的对称轴的形式，写出对称轴，根据正弦曲线的增区间，写出函数的增区间．
【考点精析】根据题目的已知条件，利用两角和与差的正弦公式和正弦函数的单调性的相关知识可以得到问题的答案，需要掌握两角和与差的正弦公式：
；正弦函数的单调性：在
上是增函数；在
上是减函数．
科目：高中数学 来源： 题型：
【题目】已知{an}为等差数列，a1+a3+a5=105，a2+a4+a6=99，以Sn表示{an}的前n项和，则使得Sn达到最大值的n是（ ）
A.21
B.20
C.19
D.18
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知四棱锥
中，底面为矩形， 
底面
， 
，
为
中点.
（Ⅰ）在图中作出平面
与
的交点
，并指出点
所在位置（不要求给出理由）；
（Ⅱ）在线段
上是否存在一点
，使得直线
与平面
所成角的正弦值为
，若存在，请说明点
的位置；若不存在，请说明理由；
（Ⅲ）求二面角
的余弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，l1，l2是通过某城市开发区中心O的两条南北和东西走向的街道，连结M、N两地之间的铁路线是圆心在l2上的一段圆弧．若点M在点O正北方向，且|MO|＝3 km，点N到l1，l2的距离分别为4 km和5 km.
(1)建立适当的坐标系，求铁路线所在圆弧的方程；
(2)若该城市的某中学拟在点O正东方向选址建分校，考虑环境问题，要求校址到点O的距离大于4 km，并且铁路线上任意一点到校址的距离不能少于
km，求该校址距点O的最近距离．(注：校址视为一个点)
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设点
为椭圆
的左焦点，直线
被椭圆
截得弦长为
．
（1）求椭圆
的方程；
（2）圆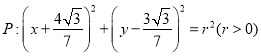
与椭圆
交于
两点， 
为线段
上任意一点，直线
交椭圆
于
两点
为圆
的直径，且直线
的斜率大于
，求
的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知命题p：x∈A，且A={x|a﹣1＜x＜a+1}，命题q：x∈B，且B={x|x2﹣4x+3≥0}
（Ⅰ）若A∩B=，A∪B=R，求实数a的值；
（Ⅱ）若p是q的充分条件，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在等比数列{an}中，a2=6，a2+a3=24，在等差数列{bn}中，b1=a1 ， b3=﹣10．
（1）求数列{an}的通项公式；
（2）求数列{bn}的前n项和Sn ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
， 
.
（Ⅰ）当
时，求曲线
在
处的切线方程；
（Ⅱ）当
时，讨论函数
的单调性；
（Ⅲ）设斜率为
的直线与函数
的图象交于
， 
两点，其中
，求证： 
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com