
【题目】将函数f(x)=cos2x﹣sin2x的图象向左平移 ![]() 个单位后得到函数F(x)的图象,则下列说法正确的是( )
个单位后得到函数F(x)的图象,则下列说法正确的是( )
A.函数F(x)是奇函数,最小值是 ![]()
B.函数F(x)是偶函数,最小值是 ![]()
C.函数F(x)是奇函数,最小值是﹣2
D.函数F(x)是偶函数,最小值是﹣2
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
【题目】随着社会的发展,食品安全问题渐渐成为社会关注的热点,为了提高学生的食品安全意识,某学校组织全校学生参加食品安全知识竞赛,成绩的频率分布直方图如图所示,数据的分组依次为[20,40),[40,60),[60,80),[80,100),若该校的学生总人数为3000,则成绩不超过60分的学生人数大约为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知△ABC三个顶点坐标为A(7,8),B(10,4),C(2,-4).
(1)求BC边上的中线所在直线的方程;
(2)求BC边上的高所在直线的方程.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)根据中点坐标公式求出![]() 中点
中点![]() 的坐标,根据斜率公式可求得
的坐标,根据斜率公式可求得![]() 的斜率,利用点斜式可求
的斜率,利用点斜式可求![]() 边上的中线所在直线的方程;(2)先根据斜率公式求出
边上的中线所在直线的方程;(2)先根据斜率公式求出![]() 的斜率,从而求出
的斜率,从而求出![]() 边上的高所在直线的斜率为
边上的高所在直线的斜率为![]() ,利用点斜式可求
,利用点斜式可求![]() 边上的高所在直线的方程.
边上的高所在直线的方程.
试题解析:(1)由B(10,4),C(2,-4),得BC中点D的坐标为(6,0),
所以AD的斜率为k=![]() =8,
=8,
所以BC边上的中线AD所在直线的方程为y-0=8(x-6),
即8x-y-48=0.
(2)由B(10,4),C(2,-4),得BC所在直线的斜率为k=![]() =1,
=1,
所以BC边上的高所在直线的斜率为-1,
所以BC边上的高所在直线的方程为y-8=-(x-7),即x+y-15=0.
【题型】解答题
【结束】
17
【题目】已知直线l:x-2y+2m-2=0.
(1)求过点(2,3)且与直线l垂直的直线的方程;
(2)若直线l与两坐标轴所围成的三角形的面积大于4,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列 ![]() 的前
的前 ![]() 项和为
项和为 ![]() ,且满足
,且满足 ![]() ,求数列
,求数列 ![]() 的通项公式.勤于思考的小红设计了下面两种解题思路,请你选择其中一种并将其补充完整.
的通项公式.勤于思考的小红设计了下面两种解题思路,请你选择其中一种并将其补充完整.
思路1:先设 ![]() 的值为1,根据已知条件,计算出
的值为1,根据已知条件,计算出 ![]() ,
, ![]() ,
, ![]() .
.
猜想: ![]() .
.
然后用数学归纳法证明.证明过程如下:
①当 ![]() 时, , 猜想成立
时, , 猜想成立
②假设 ![]() (
( ![]() N*)时,猜想成立,即
N*)时,猜想成立,即 ![]() .
.
那么,当 ![]() 时,由已知
时,由已知 ![]() ,得
,得 ![]() .
.
又 ![]() ,两式相减并化简,得
,两式相减并化简,得 ![]() (用含
(用含 ![]() 的代数式表示).
的代数式表示).
所以,当 ![]() 时,猜想也成立.
时,猜想也成立.
根据①和②,可知猜想对任何 ![]() N*都成立.
N*都成立.
思路2:先设 ![]() 的值为1,根据已知条件,计算出
的值为1,根据已知条件,计算出 ![]() .
.
由已知 ![]() ,写出
,写出 ![]() 与
与 ![]() 的关系式:
的关系式: ![]() ,
,
两式相减,得 ![]() 与
与 ![]() 的递推关系式:
的递推关系式: ![]() .
.
整理: ![]() .
.
发现:数列 ![]() 是首项为 , 公比为的等比数列.
是首项为 , 公比为的等比数列.
得出:数列 ![]() 的通项公式
的通项公式 ![]() , 进而得到
, 进而得到 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的一系列对应值如下表:
的一系列对应值如下表:

(1)根据表格提供的数据求出函数![]() 的一个解析式;
的一个解析式;
(2)根据(1)的结果,若函数![]() 的周期为
的周期为![]() ,当
,当![]() 时,方程
时,方程![]() 恰有两个不同的解,求实数
恰有两个不同的解,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市对大学生毕业后自主创业人员给予小额贷款补贴,贷款期限分为6个月、12个月、18个月、24个月、36个月五种,对于这五种期限的贷款政府分别补贴200元、300元、300元、400元、400元,从2016年享受此项政策的自主创业人员中抽取了100人进行调查统计,选取贷款期限的频数如表:
贷款期限 | 6个月 | 12个月 | 18个月 | 24个月 | 36个月 |
频数 | 20 | 40 | 20 | 10 | 10 |
以上表中各种贷款期限的频数作为2017年自主创业人员选择各种贷款期限的概率.
(Ⅰ)某大学2017年毕业生中共有3人准备申报此项贷款,计算其中恰有两人选择贷款期限为12个月的概率;
(Ⅱ)设给某享受此项政策的自主创业人员补贴为X元,写出X的分布列;该市政府要做预算,若预计2017年全市有600人申报此项贷款,则估计2017年该市共要补贴多少万元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从2017年1月18日开始,支付宝用户可以通过“![]() 扫‘福’字”和“参与蚂蚁森林”两种方式获得福卡(爱国福、富强福、和谐福、友善福,敬业福),除夕夜
扫‘福’字”和“参与蚂蚁森林”两种方式获得福卡(爱国福、富强福、和谐福、友善福,敬业福),除夕夜![]() ,每一位提前集齐五福的用户都将获得一份现金红包.某髙校一个社团在年后开学后随机调査了80位该校在读大学生,就除夕夜
,每一位提前集齐五福的用户都将获得一份现金红包.某髙校一个社团在年后开学后随机调査了80位该校在读大学生,就除夕夜![]() 之前是否集齐五福进行了一次调查(若未参与集五福的活动,则也等同于未集齐五福),得到具体数据如下表:
之前是否集齐五福进行了一次调查(若未参与集五福的活动,则也等同于未集齐五福),得到具体数据如下表:
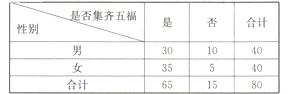
(1)计算这80位大学生集齐五福的频率,并据此估算该校10000名在读大学生中集齐五福的人数;
(2)为了解集齐五福的大学生明年是否愿意继续参加集五福活动,该大学的学生会从集齐五福的学生中,选取2位男生和3位女生逐个进行采访,最后再随机选取3次采访记录放到该大学的官方网站上,求最后被选取的3次采访对象中至少有一位男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题p:x∈(﹣∞,0),2x>3x;命题q:x∈(0,+∞), ![]() >x3; 则下列命题中真命题是( )
>x3; 则下列命题中真命题是( )
A.p∧q
B.(¬p)∧q
C.(¬p)∨(¬q)
D.p∧(¬q)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 f(x)=asinx﹣bcosx(a,b为常数,a≠0,x∈R)在x= ![]() 处取得最小值,则函数g(x)=f(
处取得最小值,则函数g(x)=f( ![]() ﹣x)是( )
﹣x)是( )
A.偶函数且它的图象关于点 (π,0)对称
B.奇函数且它的图象关于点 (π,0)对称
C.奇函数且它的图象关于点( ![]() . ,0)对称
. ,0)对称
D.偶函数且它的图象关于点( ![]() ,0)对称
,0)对称
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com