Question

19．（1）在极坐标系Ox中，设集合A={（ρ，θ）|0≤θ≤$\frac{π}{4}$，0≤ρ≤cosθ}，求集合A所表示的区域的面积；
（2）在直角坐标系xOy中，直线l₁$\left\{\begin{array}{l}{x=-4+tcos\frac{π}{4}}\\{y=tsin\frac{π}{4}}\end{array}\right.$（t为参数），曲线C₁$\left\{\begin{array}{l}{x=acosθ}\\{y=2sinθ}\end{array}\right.$（θ表示参数），其中a＞0，若曲线C上所有点均在直线l的右下方，求a的取值范围．

Answer 1

分析 （1）首先，化为直角坐标系，得到所以集合A所表示的区域为：由射线y=x（x≥0），y=0（x≥0），圆（x-$\frac{1}{2}$）²+y²=$\frac{1}{4}$所围成的区域，解得即可．
（2）首先，将直线和椭圆化为普通方程，然后，结合直线与椭圆的位置关系求解．

解答 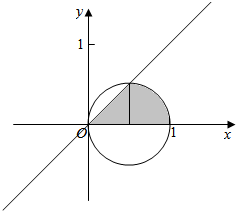解：（1）在ρ=cosθ两边同乘ρ，得ρ²=ρcos θ，化成直角坐标方程，得x²+y²=x，即（x-$\frac{1}{2}$）²+y²=$\frac{1}{4}$．
所以集合A所表示的区域为：由射线y=x（x≥0），y=0（x≥0），圆（x-$\frac{1}{2}$）²+y²=$\frac{1}{4}$所围成的区域，如图所示的阴影部分，所求面积为$\frac{1}{2}×\frac{1}{2}×\frac{1}{2}$+$\frac{1}{4}$×$\frac{π}{4}$=$\frac{1}{8}$+$\frac{π}{16}$．
（2）根据直线l：直线l₁$\left\{\begin{array}{l}{x=-4+tcos\frac{π}{4}}\\{y=tsin\frac{π}{4}}\end{array}\right.$（t为参数），得x-y+4=0，
∵曲线C₁$\left\{\begin{array}{l}{x=acosθ}\\{y=2sinθ}\end{array}\right.$（θ表示参数），曲线C：（θ为参数），
∴$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{4}$=1，
联立方程组，得
（4+a²）x²+8a²x+12a²=0，
∴△=64a⁴-4×12a²×（4+a²）＜0，
∴-2$\sqrt{3}$＜a＜2$\sqrt{3}$，
∵a＞0，
∴0＜a＜2，
∴a的取值范围（0，2$\sqrt{3}$）．

点评 本题重点考查了直线的参数方程、椭圆的参数方程等知识，直线与椭圆的位置关系等知识，属于中档题．