
【题目】已知函数
![]()
(1)在给定直角坐标系内直接画出![]() 的草图(不用列表描点),并由图象写出函数
的草图(不用列表描点),并由图象写出函数![]() 的单调减区间;
的单调减区间;
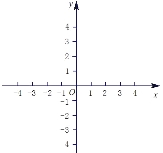
(2)当![]() 为何值时
为何值时![]() 有三个不同的零点。
有三个不同的零点。
 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知椭圆![]() 短轴的两个顶点与右焦点的连线构成等边三角形,直线
短轴的两个顶点与右焦点的连线构成等边三角形,直线![]() 与圆
与圆![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
(2)已知椭圆![]() 的左顶点
的左顶点![]() 的两条直线
的两条直线![]() 分别交椭圆
分别交椭圆![]() 于
于![]() 两点,且
两点,且![]() ,求证:直线
,求证:直线![]() 过定点,并求出定点坐标;
过定点,并求出定点坐标;
(3)在(2)的条件下求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度![]() (单位:千米时)是车流密度
(单位:千米时)是车流密度![]() (单位:辆千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/时.研究表明:当
(单位:辆千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/时.研究表明:当![]() 时,车流速度
时,车流速度![]() 是车流密度
是车流密度![]() 的一次函数.
的一次函数.
(1)当![]() 时,求函数
时,求函数![]() 的表达式;
的表达式;
(2)当车流密度![]() 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/时
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/时![]() )可以达到最大,并求出最大值.(精确到1辆/时)
)可以达到最大,并求出最大值.(精确到1辆/时)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:①若![]() (其中
(其中![]() )是偶函数, 则实数
)是偶函数, 则实数![]() ;
;
②![]() 既是奇函数又是偶函数;③若
既是奇函数又是偶函数;③若![]() ,当
,当![]()
时,![]() ,则
,则![]() ;④已知
;④已知![]() 是定义在
是定义在![]() 上的不恒为零的函数, 且对任意的
上的不恒为零的函数, 且对任意的
![]() 都满足
都满足![]() , 则
, 则![]() 是奇函数。其中所有正确命题的序号是
是奇函数。其中所有正确命题的序号是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题一定正确的是( )
A. 三点确定一个平面 B. 依次首尾相接的四条线段必共面
C. 直线与直线外一点确定一个平面 D. 两条直线确定一个平面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小型餐馆一天中要购买![]() ,
,![]() 两种蔬菜,
两种蔬菜,![]() ,
,![]() 蔬菜每公斤的单价分别为2元和3元.根据需要
蔬菜每公斤的单价分别为2元和3元.根据需要![]() 蔬菜至少要买6公斤,
蔬菜至少要买6公斤,![]() 蔬菜至少要买4公斤,而且一天中购买这两种蔬菜的总费用不能超过60元.如果这两种蔬菜加工后全部卖出,
蔬菜至少要买4公斤,而且一天中购买这两种蔬菜的总费用不能超过60元.如果这两种蔬菜加工后全部卖出,![]() ,
,![]() 两种蔬菜加工后每公斤的利润分别为2元和1元,餐馆如何采购这两种蔬菜使得利润最大,利润最大为多少元?
两种蔬菜加工后每公斤的利润分别为2元和1元,餐馆如何采购这两种蔬菜使得利润最大,利润最大为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,直三棱柱![]() 的底面为正三角形,
的底面为正三角形,![]() 分别是
分别是![]() 的中点.
的中点.
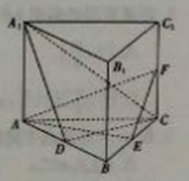
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 为
为![]() 中点,
中点,![]() 且
且![]() ,设三棱锥
,设三棱锥![]() 的体积为
的体积为![]() ,三棱锥
,三棱锥![]() 与三棱锥
与三棱锥![]() 的公共部分的体积为
的公共部分的体积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得![]() =80,
=80, ![]() =20,
=20, ![]() =184,
=184, ![]() =720.
=720.
(Ⅰ)求家庭的月储蓄y对月收入x的线性回归方程y=bx+a;
(Ⅱ)判断变量x与y之间是正相关还是负相关;
(Ⅲ)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com