
【题目】已知函数![]() ,
,![]() .
.
(1)求函数![]() 在
在![]() 上的最小值;
上的最小值;
(2)求函数![]() 在
在![]() 上的最小值;
上的最小值;
(3)求函数![]() 在
在![]() 上的值域.
上的值域.
【答案】(1)![]() ;(2)
;(2)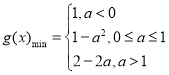 ;(3)当
;(3)当![]() 时,
时,![]() 值域为
值域为![]() ,
,![]() 时,
时,![]() 值域为
值域为![]() ,当
,当![]() 时,
时,![]() 值域为
值域为![]() ,
,![]() 时
时![]() 值域为
值域为![]() ,
,![]() 时
时![]() 值域为
值域为![]() ,
,![]() 时
时![]() 值域为
值域为![]() .
.
【解析】
(1)确定![]() 在
在![]() 上的单调性,然后可得最小值;
上的单调性,然后可得最小值;
(2)分类讨论,根据对称轴与区间![]() 关系分类;
关系分类;
(3)根据复合函数的单调性分类求解.注意函数的定义域.
(1)![]()
![]() ,函数在
,函数在![]() 上单调递减,∴
上单调递减,∴![]() ;
;
(2)![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
综上 .
.
(3)![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 时,
时,![]() 时,
时,![]() 值域为
值域为![]() ,
,![]() 时,
时,![]() 值域为
值域为![]() ,当
,当![]() 时,
时,![]() 值域为
值域为![]() ,
,![]() 时,
时,![]() 的值域是
的值域是![]() ,
,
由(1)![]() 在
在![]() 和
和![]() 上都是递减,
上都是递减,
显然当![]() 时,
时,![]() ,
,
∴当![]() 时,
时,![]() 值域为
值域为![]() ,
,![]() 时,
时,![]() 值域为
值域为![]() ,当
,当![]() 时,
时,![]() 值域为
值域为![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 值域为
值域为![]() ,
,
![]() 时,
时,![]() ,取
,取![]() ,
,![]() 值域为
值域为![]() ,
,
当![]() 时,
时,![]() ,取
,取![]() 和
和![]() ,
,![]() 值域为
值域为![]() .
.
综上,当![]() 时,
时,![]() 值域为
值域为![]() ,
,![]() 时,
时,![]() 值域为
值域为![]() ,当
,当![]() 时,
时,![]() 值域为
值域为![]() ,
,![]() 时
时![]() 值域为
值域为![]() ,
,![]() 时
时![]() 值域为
值域为![]() ,
,![]() 时
时![]() 值域为
值域为![]() .
.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:
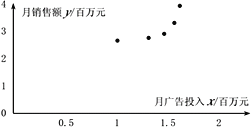
【题目】长沙某公司对其主推产品在过去5个月的月广告投入xi(百万元)和相应的销售额yi(百万元)进行了统计,其中i=1,2,3,4,5,对所得数据进行整理,绘制散点图并计算出一些统计量如下:
|
|
|
|
|
|
|
68 | 10.3 | 15.8 | -192.12 | 1.602 | 0.46 | 3.56 |
其中![]() ,i=1,2,3,4,5.
,i=1,2,3,4,5.
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为月销售额关于月广告投入xi的回归方程类型?(给出判断即可,不必说明理由)
哪一个适宜作为月销售额关于月广告投入xi的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及题中所给数据,建立y关于x的回归方程,并据此估计月广告投入200万元时的月销售额.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: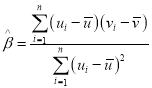 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象关于直线
的图象关于直线![]() 对称,且图象上相邻两个最高点的距离为
对称,且图象上相邻两个最高点的距离为![]() .
.
(1)求![]() 和
和![]() 的值;
的值;
(2)当![]() 时,求函数
时,求函数![]() 的最大值和最小值;
的最大值和最小值;
(3)设![]() ,若
,若![]() 的任意一条对称轴与x轴的交点的横坐标不属于区间
的任意一条对称轴与x轴的交点的横坐标不属于区间![]() ,求c的取值范围.
,求c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)求证:![]()
(2)若函数![]() 的图象与直线
的图象与直线![]() 没有交点,求实数
没有交点,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() ,则是否存在实数
,则是否存在实数![]() ,使得
,使得![]() 的最小值为
的最小值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
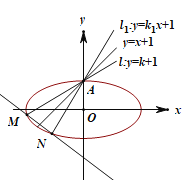
【题目】如图,直线![]() (
(![]() )关于直线
)关于直线![]() 对称的直线为
对称的直线为![]() ,直线
,直线![]() ,
,![]() 与椭圆
与椭圆![]() 分别交于点A,M和A,N,记直线
分别交于点A,M和A,N,记直线![]() 的斜率为
的斜率为![]() .
.
(1)求![]() 的值;
的值;
(2)当![]() 变化时,直线
变化时,直线![]() 是否恒过定点?若恒过定点,求出该定点坐标;若不恒过定点,请说明理由.
是否恒过定点?若恒过定点,求出该定点坐标;若不恒过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】类比平面几何中的定理:△ABC中,若DE是△ABC的中位线,则有S△ADE∶S△ABC=1∶4;若三棱锥A-BCD有中截面EFG∥平面BCD,则截得三棱锥的体积与原三棱锥体积之间的关系式为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有编号为1,2,3…n的n个学生,入座编号为1,2,3…n的n个座位,每个学生规定坐一个座位, 设学生所坐的座位号与该生的编号不同的学生人数为![]() , 已知
, 已知![]() 时, 共有6种坐法.
时, 共有6种坐法.
(1)求![]() 的值;
的值;
(2)求随机变量![]() 的概率分布列及数学期望
的概率分布列及数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com