
分析 函数g(x)=f(x)-($\frac{1}{2}$)x-a在区间(-2,6]上恰有3个不同零点?函数y=f(x)与函数y=$(\frac{1}{2})^{x}+a$在区间(-2,6]上恰有3个不同交点点; 依据函数y=f(x)周期、当x∈[0,2]时,f(x)=2x-1及f(x)的奇偶性,可画出数y=f(x)在区间(-2,6]上的图象,结合图象求解.
解答 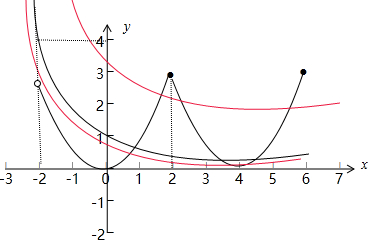 解:函数g(x)=f(x)-($\frac{1}{2}$)x-a在区间(-2,6]上恰有3个不同零点?函数y=f(x)与函数y=$(\frac{1}{2})^{x}+a$在区间(-2,6]上恰有3个不同交点点;
解:函数g(x)=f(x)-($\frac{1}{2}$)x-a在区间(-2,6]上恰有3个不同零点?函数y=f(x)与函数y=$(\frac{1}{2})^{x}+a$在区间(-2,6]上恰有3个不同交点点;
∵函数f(x)是定义在R上,且对于所有的x都有f(x+2)=f(x-2)恒成立,∴函数y=f(x)周期为4,
由当x∈[0,2]时,f(x)=2x-1及f(x)的奇偶性,可画出数y=f(x)在区间(-2,6]上的图象,如下
只需$(\frac{1}{2})^{2}+a<3,(\frac{1}{2})^{4}+a>0$即可,解得-$\frac{1}{16}$<a$<\frac{11}{4}$.
故答案为:(-$\frac{1}{16},\frac{11}{4}$)
点评 本题考查了函数零点问题,考查了函数与方程的思想、数形结合思想,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
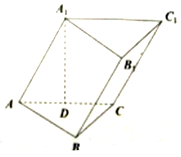 如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1是边长为4的菱形,BC⊥平面ACC1A1,CB=2,点A1在底面ABC上的射影D为棱AC的中点,点A在平面A1CB内的射影为E.
如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1是边长为4的菱形,BC⊥平面ACC1A1,CB=2,点A1在底面ABC上的射影D为棱AC的中点,点A在平面A1CB内的射影为E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最大值$-4\sqrt{3}$ | B. | 最小值$-4\sqrt{3}$ | C. | 最大值$4\sqrt{3}$ | D. | 最小值$4\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
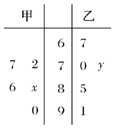 某机械厂今年进行了五次技能考核,其中甲、乙两名技术骨干得分的平均分相等,成绩统计情况如茎叶图所示(其中a是0~9的某个整数);
某机械厂今年进行了五次技能考核,其中甲、乙两名技术骨干得分的平均分相等,成绩统计情况如茎叶图所示(其中a是0~9的某个整数);查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分数区间 | [50,70] | [70,90] | [90,110] | [110,130] | [130,150] |
| 人数 | 2 | 8 | 32 | 38 | 20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com