
 设全集为U=R,集合A={x|(x+3)(x-6)≤0},B={x|log2(x+2)<4}.
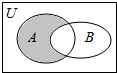
设全集为U=R,集合A={x|(x+3)(x-6)≤0},B={x|log2(x+2)<4}.分析 (1)利用Venn图表示集合的关系即可求如图阴影部分表示的集合;
(2)根据集合关系C⊆B,建立不等式关系即可求实数a的取值范围.
解答 解:(1)由(x+3)(x-6)≤0,得-3≤x≤6,即A=[-3,6],
由0<x+2<16,解得-2<x<14,即B=(-2,14),
∵阴影部分为A∩CRB,
∴A∩CRB=[-3,-2].
(2)∵C={x|x>2a且x<a+1},
∴①2a≥a+1,即a≥1时,C=∅,成立;
②2a<a+1,即a<1时,C=(2a,a+1)⊆(-2,14),
则$\left\{\begin{array}{l}{a+1≤14}\\{2a≥-2}\end{array}\right.$,
解得-1≤a<1.
综上所述,a的取值范围为[-1,+∞).
点评 本题主要考查集合的基本运算以及集合的基本关系的应用,利用Venn图表示集合关系是解决本题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
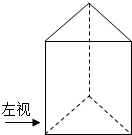 如图,侧棱长为2a的正三棱柱的左视图的面积为$\sqrt{3}$a2,则该正三棱柱的侧面积为( )
如图,侧棱长为2a的正三棱柱的左视图的面积为$\sqrt{3}$a2,则该正三棱柱的侧面积为( )| A. | 3a2 | B. | 4a2 | C. | 6a2 | D. | 8a2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=($\sqrt{x}$)2,g(x)=x | B. | f(x)=$\frac{{x}^{2}}{x}$,g(x)=x | C. | f(x)=$\sqrt{{x}^{2}}$,g(x)=$\root{3}{{x}^{3}}$ | D. | f(x)=$\root{6}{{x}^{3}}$,g(x)=$\sqrt{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1] | B. | (0,2) | C. | $({0,2\sqrt{3}})$ | D. | (0,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 9 | C. | 6 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=\frac{x^2}{x}$与y=x | B. | $y=\sqrt{x^2}$与y=x | C. | y=x0与y=1 | D. | $y=\root{3}{x^3}$与y=x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com