
【题目】设双曲线C的焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,其一个顶点的坐标是(0,1).
,其一个顶点的坐标是(0,1).
(Ⅰ)求双曲线C的标准方程;
(Ⅱ)若直线![]() 与该双曲线交于A、B两点,且A、B的中点为(2,3),求直线
与该双曲线交于A、B两点,且A、B的中点为(2,3),求直线![]() 的方程
的方程
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:
【题目】网购已经成为一种时尚,商家为了鼓励消费,购买时在店铺领取优惠券,买后给予好评返还现金等促销手段.经统计,近五年某店铺用于促销的费用![]() (万元)与当年度该店铺的销售收人
(万元)与当年度该店铺的销售收人![]() (万元)的数据如下表:
(万元)的数据如下表:
年份 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 |
促销费用 |
|
|
|
|
|
销售收入 |
|
|
|
|
|
(1)请根据上表提供的数据,用最小二乘法求出/span>![]() 关于
关于![]() 的线性回归方
的线性回归方![]() ;
;
(2)2018年度该店铺预测销售收人至少达到![]() 万元,则该店铺至少准备投入多少万元的促销费?
万元,则该店铺至少准备投入多少万元的促销费?
参考公式:
参考数据: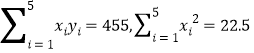
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求![]() 的值;
的值;
(2)若函数![]() 在区间
在区间![]() 是单调递增函数,求实数
是单调递增函数,求实数![]() 的取值范围;
的取值范围;
(3)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 内有两个实数根
内有两个实数根![]() ,记
,记![]() ,求实数
,求实数![]() 的取值范围 .
的取值范围 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个几何体,它的下面是一个圆柱,上面是一个圆锥,并且圆锥的底面与圆柱的上底面重合,圆柱的底面直径为3 cm,高为4 cm,圆锥的高为3 cm,画出此几何体的直观图.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知任意角
中,已知任意角![]() 以坐标原点
以坐标原点![]() 为顶点,
为顶点,![]() 轴的非负半轴为始边,若终边经过点
轴的非负半轴为始边,若终边经过点![]() ,且
,且![]() ,定义:
,定义:![]() ,称“
,称“![]() ”为“正余弦函数”,对于“正余弦函数
”为“正余弦函数”,对于“正余弦函数![]() ”,有同学得到以下性质:
”,有同学得到以下性质:
①该函数的值域为![]() ; ②该函数的图象关于原点对称;
; ②该函数的图象关于原点对称;
③该函数的图象关于直线![]() 对称; ④该函数为周期函数,且最小正周期为
对称; ④该函数为周期函数,且最小正周期为![]() ;
;
⑤该函数的递增区间为![]() .
.
其中正确的是__________.(填上所有正确性质的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,![]() 是临江公园内一个等腰三角形形状的小湖(假设湖岸是笔直的),其中两腰
是临江公园内一个等腰三角形形状的小湖(假设湖岸是笔直的),其中两腰![]() 米,
米,![]() .为了给市民营造良好的休闲环境,公园管理处决定在湖岸
.为了给市民营造良好的休闲环境,公园管理处决定在湖岸![]() ,
,![]() 上分别取点
上分别取点![]() ,
,![]() (异于线段端点),在湖上修建一条笔直的水上观光通道
(异于线段端点),在湖上修建一条笔直的水上观光通道![]() (宽度不计),使得三角形
(宽度不计),使得三角形![]() 和四边形
和四边形![]() 的周长相等.
的周长相等.

(1)若水上观光通道的端点![]() 为线段
为线段![]() 的三等分点(靠近点
的三等分点(靠近点![]() ),求此时水上观光通道
),求此时水上观光通道![]() 的长度;
的长度;
(2)当![]() 为多长时,观光通道
为多长时,观光通道![]() 的长度最短?并求出其最短长度.
的长度最短?并求出其最短长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表。

A地区用户满意度评分的频率分布直方图

B地区用户满意度评分的频数分布表
(Ⅰ)在答题卡上作出B地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可);
(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个等级:
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
估计哪个地区的满意度等级为不满意的概率大?说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱台ABCDEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.
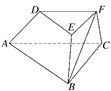
(1)求证:BF⊥平面ACFD;
(2)求二面角B-AD-F的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司近年来科研费用支出![]() 万元与公司所获利润
万元与公司所获利润![]() 万元之间有如表的统计
万元之间有如表的统计
![]()
数据:参考公式:用最小二乘法求出![]() 关于
关于![]() 的线性回归方程为:
的线性回归方程为: ![]() ,
,
其中: 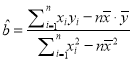 ,
, ![]() ,参考数值:
,参考数值: ![]() 。
。
(Ⅰ)求出![]() ;
;
(Ⅱ)根据上表提供的数据可知公司所获利润![]() 万元与科研费用支出
万元与科研费用支出![]() 万元线性相关,请用最小二乘法求出
万元线性相关,请用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅲ)试根据(Ⅱ)求出的线性回归方程,预测该公司科研费用支出为10万元时公司所获得的利润。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com