
【题目】对于函数![]() ,如果存在实数
,如果存在实数![]() (
(![]() ,且
,且![]() 不同时成立),使得
不同时成立),使得![]() 对
对![]() 恒成立,则称函数
恒成立,则称函数![]() 为“
为“![]() 映像函数”.
映像函数”.
(1)判断函数![]() 是否是“
是否是“![]() 映像函数”,如果是,请求出相应的
映像函数”,如果是,请求出相应的![]() 的值,若不是,请说明理由;
的值,若不是,请说明理由;
(2)已知函数![]() 是定义在
是定义在![]() 上的“
上的“![]() 映像函数”,且当
映像函数”,且当![]() 时,
时,![]() .求函数
.求函数![]() (
(![]() )的反函数;
)的反函数;
(3)在(2)的条件下,试构造一个数列![]() ,使得当
,使得当![]() 时,
时,![]() ,并求
,并求![]() 时,函数
时,函数![]() 的解析式,及
的解析式,及![]() 的值域.
的值域.
【答案】(1)![]() 是“
是“![]() 映像函数”,
映像函数”,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,值域
,值域![]()
【解析】
(1)直接由题意列关于a,b的方程组,求解得答案;
(2)由题意可得f(0)=f(3),f(1)=f(7),而当x∈[0,1)时,f(x)=2x,则x∈[3,7)时,设f(x)=2sx+t,可得![]() ,求得s,t的值,则函数解析式可求,把x用含有y的代数式表示,把x,y互换可得y=f(x)(x∈[3,7))的反函数;
,求得s,t的值,则函数解析式可求,把x用含有y的代数式表示,把x,y互换可得y=f(x)(x∈[3,7))的反函数;
(3)由(2)可知,构造数列{an},满足a1=0,an+1=2an+1,可得数列{an+1}是以1为首项,以2为公比的等比数列,由此求得![]() .当x∈[an,an+1)=[2n﹣1﹣1,2n﹣1),令
.当x∈[an,an+1)=[2n﹣1﹣1,2n﹣1),令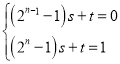 ,解得s=21﹣n,t=21﹣n﹣1,可得x∈[an,an+1)(n∈N*)时,函数y=f(x)的解析式为f(x)
,解得s=21﹣n,t=21﹣n﹣1,可得x∈[an,an+1)(n∈N*)时,函数y=f(x)的解析式为f(x)![]() ,并求得x∈[0,+∞)时,函数f(x)的值域为[1,2).
,并求得x∈[0,+∞)时,函数f(x)的值域为[1,2).
(1)对于![]() ,
,![]() ,
,
若![]() ,则
,则![]() ,
,
即![]() 恒成立,∴
恒成立,∴![]() ,∵
,∵![]() 不同时成立,∴
不同时成立,∴![]() ,
,
即![]() 是“
是“![]() 映像函数”
映像函数”
(2)当![]() 时,
时,![]() ,从而
,从而![]() ,∵函数
,∵函数![]() 是定义在
是定义在![]() 上的“
上的“![]() 映像函数”,
映像函数”,
∴![]() ,令
,令![]() ,则
,则![]() ,∴
,∴![]()
∴![]() (
(![]() ),由
),由![]() 得,
得,![]() ,此时
,此时![]()
∴当![]() 时,函数
时,函数![]() 的反函数是
的反函数是![]() ;
;
(3)∵![]() 时,
时,![]() ,
,
∴构造数列![]() ,
,![]() ,且
,且![]() ,于是
,于是![]() ,
,
∴![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列,∴
为公比的等比数列,∴![]() ,
,
而![]()
∴当![]() ,即
,即![]() 时,
时,![]()
对于函数![]() ,∵
,∵![]() ,令
,令![]() ,则
,则![]()
∴![]() ,
,![]()
∴当![]() 时,
时,![]() ,
,
函数![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]()
而![]()
![]() ,
,
即函数![]() 的值域为
的值域为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】2019年1月1日新修订的个税法正式实施,规定:公民全月工资、薪金所得不超过5000元的部分不必纳税,超过5000元的部分为全月应纳税所得额.此项税款按下表分段累计计算(预扣):
全月应缴纳所得额 | 税率 |
不超过3000元的部分 |
|
超过3000元至12000元的部分 |
|
超过12000元至25000元的部分 |
|
国家在实施新个税时,考虑到纳税人的实际情况,实施了《个人所得税税前专项附加扣税暂行办法》,具体如下表:
项目 | 每月税前抵扣金额(元) | 说明 |
子女教育 | 1000 | 一年按12月计算,可扣12000元 |
继续教育 | 400 | 一年可扣除4800元,若是进行技能职业教育或者专业技术职业资格教育一年可扣除3600元 |
大病医疗 | 5000 | 一年最高抵扣金额为60000元 |
住房贷款利息 | 1000 | 一年可扣除12000元,若夫妻双方在同一城市工作,可以选择一方来扣除 |
住房租金 | 1500/1000/800 | 扣除金额需要根据城市而定 |
2000 | 一年可扣除24000元,若不是独生子女,子女平均扣除.赡养老人年龄需要在60周岁及以上 |
老李本人为独生子女,家里有70岁的老人需要赡养,有一个女儿正读高三,他每月还需缴纳住房贷款2734元.若2019年11月老李工资,薪金所得为20000元,按照《个人所得税税前专项附加扣税暂行办法》,则老李应缴纳税款(预扣)为______元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]()
(![]() )求数列
)求数列![]() 的通项公式;
的通项公式;
(![]() )若数列
)若数列![]() 满足
满足![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(![]() )在(
)在(![]() )的条件下,设
)的条件下,设![]() ,问是否存在实数
,问是否存在实数![]() 使得数列
使得数列![]() 是单调递增数列?若存在,求出
是单调递增数列?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数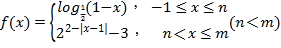 的值域是
的值域是![]() ,有下列结论:①当
,有下列结论:①当![]() 时,
时,![]() ; ②当
; ②当![]() 时,
时,![]() ;③当
;③当![]() 时,
时,![]() ; ④当
; ④当![]() 时,
时,![]() .其中结论正确的所有的序号是( ).
.其中结论正确的所有的序号是( ).
A.①②B.③④C.②③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() 的图像与函数
的图像与函数![]() 的图像关于直线
的图像关于直线![]() 对称.
对称.
(1)求函数![]() 的解析式;
的解析式;
(2)若函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)设函数![]() ,试用列举法表示集合
,试用列举法表示集合![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为提高市场销售业绩,设计了一套产品促销方案,并在某地区部分营销网点进行试点.运作一年后,对“采取促销”和“没有采取促销”的营销网点各选了50个,对比上一年度的销售情况,分别统计了它们的年销售总额,并按年销售总额增长的百分点分成5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,分别统计后制成如图所示的频率分布直方图,并规定年销售总额增长10个百分点及以上的营销网点为“精英店”.
,分别统计后制成如图所示的频率分布直方图,并规定年销售总额增长10个百分点及以上的营销网点为“精英店”.
“采用促销”的销售网点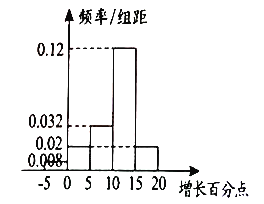
“不采用促销”的销售网点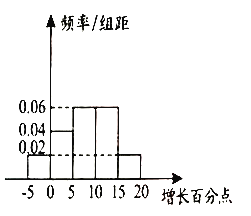
(1)请根据题中信息填充下面的列联表,并判断是否有![]() 的把握认为“精英店与采促销活动有关”;
的把握认为“精英店与采促销活动有关”;
采用促销 | 无促销 | 合计 | |
精英店 | |||
非精英店 | |||
合计 | 50 | 50 | 100 |
(2)某“精英店”为了创造更大的利润,通过分析上一年度的售价![]() (单位:元)和日销量
(单位:元)和日销量![]() (单位:件)(
(单位:件)(![]() )的一组数据后决定选择
)的一组数据后决定选择![]() 作为回归模型进行拟合.具体数据如下表,表中的
作为回归模型进行拟合.具体数据如下表,表中的![]()
|
|
|
|
|
|
|
45.8 | 395.5 | 2413.5 | 4.6 | 21.6 |
|
|
①根据上表数据计算![]() ,
,![]() 的值;
的值;
②已知该公司产品的成本为10元/件,促销费用平均5元/件,根据所求出的回归模型,分析售价![]() 定为多少时日利润
定为多少时日利润![]() 可以达到最大.
可以达到最大.
附①: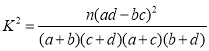
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
附②:对应一组数据![]() ,
,
其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为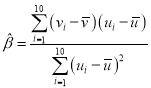 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() .
.

(1)求证:![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值?若不存在,说明理由.
的值?若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分形几何学是数学家伯努瓦曼德尔布罗在20世纪70年代创立的一门新的数学学科.它的创立为解决传统科学众多领域的难题提供了全新的思路.按照如图1所示的分形规律可得如图2所示的一个树形图:
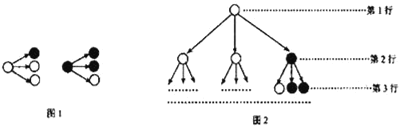
易知第三行有白圈5个,黑圈4个.我们采用“坐标”来表示各行中的白圈、黑圈的个数.比如第一行记为![]() ,第二行记为
,第二行记为![]() ,第三行记为
,第三行记为![]() .照此规律,第
.照此规律,第![]() 行中的白圈、黑圈的“坐标”为
行中的白圈、黑圈的“坐标”为![]() ,则
,则![]() ________.
________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com