
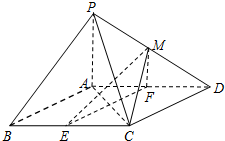
 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=6,E,F分别为BC,AD的中点,点M在线段PD上.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=6,E,F分别为BC,AD的中点,点M在线段PD上.分析 (Ⅰ)证明AB⊥AC.得到EF⊥AC.证明PA⊥底面ABCD,可得PA⊥EF.然后证明EF⊥平面PAC.
(Ⅱ)证明MF∥PA,即可证明MF∥平面PAB,同理EF∥平面PAB.然后证明平面MEF∥平面PAB,得到ME∥平面PAB.
(Ⅲ)证明MN⊥底面ABCD,然后求解四棱锥M-ECDF的体积.
解答  (本小题满分14分)
(本小题满分14分)
(Ⅰ)证明:在平行四边形ABCD中,因为AB=AC,∠BCD=135°,
∴∠ABC=45°,
所以AB⊥AC.
由E,F分别为BC,AD的中点,得EF∥AB,
所以EF⊥AC.…(1分)
因为侧面PAB⊥底面ABCD,且∠BAP=90°,
所以PA⊥底面ABCD.…(2分)
又因为EF?底面ABCD,
所以PA⊥EF.…(3分)
又因为PA∩AC=A,PA?平面PAC,AC?平面PAC,
所以EF⊥平面PAC.…(5分)
(Ⅱ)证明:因为M为PD的中点,F分别为AD的中点,
所以MF∥PA,
又因为MF?平面PAB,PA?平面PAB,
所以MF∥平面PAB.…(7分)
同理,得EF∥平面PAB.
又因为MF∩EF=F,MF?平面MEF,EF?平面MEF,
所以平面MEF∥平面PAB.…(9分)
又因为ME?平面MEF,
所以ME∥平面PAB.…(10分)
(Ⅲ)解:在△PAD中,过M作MN∥PA交AD于点N(图略),
由$\frac{PM}{MD}=\frac{1}{2}$,得$\frac{MN}{PA}=\frac{2}{3}$,
又因为PA=6,
所以MN=4,…(12分)
因为PA⊥底面ABCD,
所以MN⊥底面ABCD,
所以四棱锥M-ECDF的体积${V_{M-ECDF}}=\frac{1}{3}×{S_{平行四边形ECDF}}×MN=\frac{1}{3}×\frac{6×6}{2}×4=24$.…(14分)
点评 本题考查直线与平面垂直与平行的判定定理以及性质定理的应用,平面与平面平行的判定定理的应用,几何体的体积的求法,考查转化思想以及计算能力.


 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源: 题型:解答题
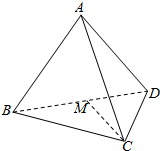 如图,在三棱锥A-BCD中,等边△BCD的边长为4,△ABD是以∠A为直角的等腰直角三角形,平面ABD⊥平面BCD,点M是棱BD的中点.
如图,在三棱锥A-BCD中,等边△BCD的边长为4,△ABD是以∠A为直角的等腰直角三角形,平面ABD⊥平面BCD,点M是棱BD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 我国是世界上严重缺水的国家之一,城市缺水问题比较突处,某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,假设采用抽样调查方式,获得了100户居民某年的月均用水量(单位:t),并用这些样本数据分成9画出频率分布直方图,其中第3、4、5、6组的高度分别是0.15、0.22、0.25、0.14,第7、8、9、组高度比为3:2:1,直方图如图:
我国是世界上严重缺水的国家之一,城市缺水问题比较突处,某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,假设采用抽样调查方式,获得了100户居民某年的月均用水量(单位:t),并用这些样本数据分成9画出频率分布直方图,其中第3、4、5、6组的高度分别是0.15、0.22、0.25、0.14,第7、8、9、组高度比为3:2:1,直方图如图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com