
【题目】选修4-4:坐标系与参数方程
在极坐标系中,圆![]() 的圆心坐标为
的圆心坐标为![]() ,半径为2.以极点为原点,极轴为
,半径为2.以极点为原点,极轴为![]() 的正半轴,取相同的长度单位建立平面直角坐标系,直线
的正半轴,取相同的长度单位建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为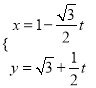 (
(![]() 为参数).
为参数).
(1)求圆![]() 的极坐标方程;
的极坐标方程;
(2)设![]() 与圆
与圆![]() 的交点为
的交点为![]() ,
, ![]() 与
与![]() 轴的交点为
轴的交点为![]() ,求
,求![]() .
.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)将参数方程转化为直角坐标系下的普通方程,需要根据参数方程的结构特征,选取恰当的消参方法,常见的消参方法有:代入消参法、加减消参法、平方消参法;(2)将参数方程转化为普通方程时,要注意两种方程的等价性,不要增解、漏解,若![]() 有范围限制,要标出
有范围限制,要标出![]() 的取值范围;(3)掌握圆的参数方程
的取值范围;(3)掌握圆的参数方程![]() ,通过圆心距和两圆半径之和、之差的关系判断圆与圆的位置关系(4)根据题意设点根据点到直线的距离公式.
,通过圆心距和两圆半径之和、之差的关系判断圆与圆的位置关系(4)根据题意设点根据点到直线的距离公式.
试题解析:解:(1)法一:在直角坐标系中,圆心的坐标为![]() ,所以圆C的方程为
,所以圆C的方程为![]() 即
即![]() , 2分
, 2分
化为极坐标方程得![]() ,即
,即![]() 4分
4分
法二:令圆![]() 上任一点
上任一点![]() ,在
,在![]() 中(其中
中(其中![]() 为极点),
为极点),![]() , 2分
, 2分
由余弦定理得![]()
从而圆![]() 的极坐标方程为
的极坐标方程为![]() 4分
4分
(2)法一:把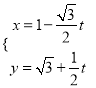 代入
代入![]() 得
得![]() ,所以点A、B对应的参数分别为
,所以点A、B对应的参数分别为![]() 5分
5分
令![]() 得点
得点![]() 对应的参数为
对应的参数为![]() 6分
6分
所以![]()
![]() 7分
7分
法二:把 化为普通方程得
化为普通方程得![]() , 5分
, 5分
令![]() 得点P坐标为
得点P坐标为![]() ,又因为直线
,又因为直线![]() 恰好经过圆
恰好经过圆![]() 的圆心
的圆心![]() ,
,
故![]() 7分
7分


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】(2017·郑州第二次质量预测)如图,高为1的等腰梯形ABCD中,AM=CD=![]() AB=1.现将△AMD沿MD折起,使平面AMD⊥平面MBCD,连接AB,AC.
AB=1.现将△AMD沿MD折起,使平面AMD⊥平面MBCD,连接AB,AC.
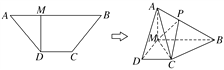
(1)在AB边上是否存在点P,使AD∥平面MPC?
(2)当点P为AB边的中点时,求点B到平面MPC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-5:不等式选讲
设函数f(x)=e2x-aln x.
(1)讨论f(x)的导函数f′(x)零点的个数;
(2)证明:当a>0时,f(x)≥2a+aln![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(1)若曲线![]() 在
在![]() 轴上的截距为
轴上的截距为![]() ,且在点
,且在点![]() 处的切线垂直于直线
处的切线垂直于直线![]() ,求实数
,求实数![]() 的值;
的值;
(2)记![]() 的导函数为
的导函数为![]() ,
, ![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,圆![]() 的圆心坐标为
的圆心坐标为![]() ,半径为2.以极点为原点,极轴为
,半径为2.以极点为原点,极轴为![]() 的正半轴,取相同的长度单位建立平面直角坐标系,直线
的正半轴,取相同的长度单位建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为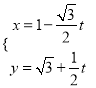 (
(![]() 为参数).
为参数).
(1)求圆![]() 的极坐标方程;
的极坐标方程;
(2)设![]() 与圆
与圆![]() 的交点为
的交点为![]() ,
, ![]() 与
与![]() 轴的交点为
轴的交点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形, ![]() , 平面
, 平面![]() 底面
底面![]() ,且
,且![]() 是边长为
是边长为![]() 的等边三角形,
的等边三角形, ![]() ,
, ![]() 是
是![]() 中点.
中点.
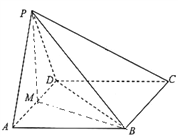
(1)求证:平面![]() 平面
平面![]() ;
;
(2)证明: ![]() , 且
, 且![]() 与
与![]() 的面积相等.
的面积相等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com