
如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝.再用S平方米塑料片制成圆柱的侧面和下底面(不安装上底面).
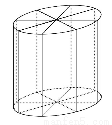
(1)当圆柱底面半径r取何值时,S取得最大值?并求出该最大值(结果精确到0.01平方米).
(2)若要制作一个如图放置的、底面半径为0.3米的灯笼,请作出灯笼的三视图(作图时,不需考虑骨架等因素).
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(一)第一章第一节练习卷(解析版) 题型:选择题
已知集合A={x|x2+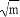 x+1=0},若A∩R=?,则实数m的取值范围是( )
x+1=0},若A∩R=?,则实数m的取值范围是( )
(A)m<4 (B)m>4
(C)0≤m<4 (D)0≤m≤4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十八第七章第七节练习卷(解析版) 题型:解答题
如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角.

求证:(1)CM∥平面PAD.
(2)平面PAB⊥平面PAD.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十五第七章第四节练习卷(解析版) 题型:解答题
在如图所示的几何体中,四边形ABCD为平行四边形,∠ACB=90°,EA⊥平面ABCD,EF∥AB,FG∥BC,EG∥AC,AB=2EF.若M是线段AD的中点,
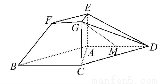
求证:GM∥平面ABFE.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十五第七章第四节练习卷(解析版) 题型:选择题
设α,β是两个不同的平面,m,n是平面α内的两条不同直线,l1,l2是平面β内的两条相交直线,则α∥β的一个充分不必要条件是( )
(A)m∥β且l1∥α (B)m∥β且n∥l2
(C)m∥β且n∥β (D)m∥l1且n∥l2
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十二第七章第一节练习卷(解析版) 题型:填空题
棱长为1的正方体ABCD-A1B1C1D1的8个顶点都在球O的表面上,若棱AA1,DD1的中点分别为E,F,则直线EF被球O截得的弦长为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十二第七章第一节练习卷(解析版) 题型:选择题
如图,模块①~⑤均由4个棱长为1的小正方体构成,模块⑥由15个棱长为1的小正方体构成.现从模块①~⑤中选出三个放到模块⑥上,使得模块⑥成为一个棱长为3的大正方体,则下列选择方案中,能够完成任务的为( )
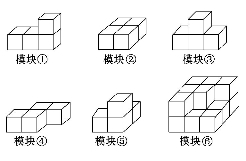
(A)模块①,②,⑤ (B)模块①,③,⑤
(C)模块②,④,⑤ (D)模块③,④,⑤
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十三第七章第二节练习卷(解析版) 题型:选择题
长方体的三个相邻面的面积分别为2,3,6,这个长方体的顶点都在同一个球面上,则这个球的表面积为( )
(A) π (B)56π (C)14π (D)64π
π (B)56π (C)14π (D)64π
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十一第六章第七节练习卷(解析版) 题型:选择题
已知f(n)=(2n+7)·3n+9,存在自然数m,使得对任意n∈N*,f(n)都能被m整除,则m的最大值为( )
(A)18 (B)36 (C)48 (D)54
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com