
 ,
,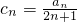 ,试判断并说明cn+1-cn(n∈N*)的符号;
,试判断并说明cn+1-cn(n∈N*)的符号;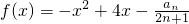 ,是否存在最大的实数λ,当x≤λ时,对于一切自然数n,都有f(x)≤0.
,是否存在最大的实数λ,当x≤λ时,对于一切自然数n,都有f(x)≤0. ,
, ,
, .
. ,
,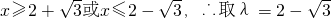 .
. ,表示出数列的前n项和公式,问题就变化为由sn求an的问题,这种问题要仿写一个sn-1,两个式子相减,得到要求的通项.注意首相是否符合通项.
,表示出数列的前n项和公式,问题就变化为由sn求an的问题,这种问题要仿写一个sn-1,两个式子相减,得到要求的通项.注意首相是否符合通项.

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com