
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π,x∈R)在一个周期内的图象如图所示,则函数的解析式为 . 直线y= ![]() 与函数y=f(x)(x∈R)图象的所有交点的坐标为 .
与函数y=f(x)(x∈R)图象的所有交点的坐标为 . 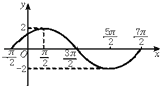
【答案】f(x)=2sin( ![]() x+
x+ ![]() );(
);( ![]() +4kπ,
+4kπ, ![]() )或(
)或( ![]() +4kπ,
+4kπ, ![]() )(k∈Z)
)(k∈Z)
【解析】解:∵f(x)=Asin(ωx+φ)(A>0,ω>0,x∈R),
∴A=2,周期T= ![]() =
= ![]() ﹣(﹣
﹣(﹣ ![]() )=4π,
)=4π,
∴ω= ![]() .
.
∴f(x)=2sin( ![]() x+φ),
x+φ),
又f(﹣ ![]() )=2sin(
)=2sin( ![]() ×(﹣
×(﹣ ![]() )+φ)=0,
)+φ)=0,
∴φ﹣ ![]() =kπ,k∈Z,|φ|<π,
=kπ,k∈Z,|φ|<π,
∴φ= ![]() .
.
∴f(x)=2sin( ![]() x+
x+ ![]() ).
).
当f(x)= ![]() 时,即2sin(
时,即2sin( ![]() x+
x+ ![]() )=
)= ![]() ,可得sin(
,可得sin( ![]() x+
x+ ![]() )=
)= ![]() ,
,
∴ ![]() x+
x+ ![]() =
= ![]() +2kπ或
+2kπ或 ![]() x+
x+ ![]() =
= ![]() +2kπ(k∈Z),可得x=
+2kπ(k∈Z),可得x= ![]() +4kπ或
+4kπ或 ![]() +4kπ(k∈Z)
+4kπ(k∈Z)
由此可得,直线y= ![]() 与函数f(x)图象的所有交点的坐标为:(
与函数f(x)图象的所有交点的坐标为:( ![]() +4kπ,
+4kπ, ![]() )或(
)或( ![]() +4kπ,
+4kπ, ![]() )(k∈Z).
)(k∈Z).
所以答案是:f(x)=2sin( ![]() x+
x+ ![]() ),(
),( ![]() +4kπ,
+4kπ, ![]() )或(
)或( ![]() +4kπ,
+4kπ, ![]() )(k∈Z).
)(k∈Z).


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C对的边分别为a,b,c,且c=2,C=60°.
(1)求 ![]() 的值;
的值;
(2)若a+b=ab,求△ABC的面积S△ABC .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C所对的边分别为a,b,c,已知a=2,b=3,cosC= ![]() .
.
(1)求△ABC的面积;
(2)求sin(C﹣A)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com