
【题目】最近的一次数学竞赛共6道试题,每题答对得7分,答错(或不答)得0分.赛后某参赛代表队获团体总分161分,且统计分数时发现:该队任两名选手至多答对两道相同的题目.没有三名选手都答对两道相同的题目.试问该队选手至少有多少人?
【答案】7
【解析】
设该队有n名选手,分别记为![]() ,记6道题的编号依次为1,2,...,6.以编号为行、选手为列作一个6×n的方格表.如果选手
,记6道题的编号依次为1,2,...,6.以编号为行、选手为列作一个6×n的方格表.如果选手![]() 答对第j(j=1,2,...,6)题,就将方格表中第j行第i列的小方格(j, i)的中心染成红点.我们的问题就是在6×n的方格表中,不存在“横”6点矩形
答对第j(j=1,2,...,6)题,就将方格表中第j行第i列的小方格(j, i)的中心染成红点.我们的问题就是在6×n的方格表中,不存在“横”6点矩形![]() 和“纵”6点矩形
和“纵”6点矩形![]() 的情况,且至少有23个红点时,求n的最小值.
的情况,且至少有23个红点时,求n的最小值.
如第1列有6个红点,那么,后面各列至多有2个红点.因为![]() ,于是,取第2至10列,其中第2至9列每列有2个红点,第10列1个红点(如图)满足题设.这说明n的最小值不大于10.
,于是,取第2至10列,其中第2至9列每列有2个红点,第10列1个红点(如图)满足题设.这说明n的最小值不大于10.

我们发现,可通过将第1列中某点移到此点所在行的其他列中来减少图6的列数,如作移动(6, 1)→(6,2),可同时作移动(4,10)→(6,3),(3,9)→(6,4),(5,9)→(6,7),这样便得到有23个红点的图7.类似地可得图8.这说明n的最小值不大于7.
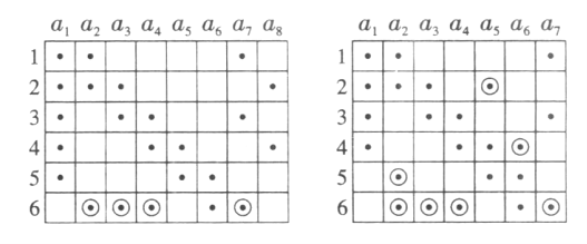
下面证明:n的最小值大于6.
对于一个恰有6列的方格表,由抽屉原理知至少有一列红点数不少于4,不妨设第1列,且第1列的前4行的小方格的中心是红点.如果某列有2个红点,则称其为某列上的一个红点“行对”.这样在前4行中,除第1列外的5列中每列只能有一个行对.于是,前4行中总共有![]() 个行对.考虑最后两行:若第1列还有红点,那么,有红点的这一行不能再有其他的红点.如第1列还有2个红点,这时能增加9个行对,6×6方格表中共有11+9=20个行对;如第1 列还有1个红点,不妨设第1列第5行的小方格有红点,这时即使第6行除第1列外的其他小方格都有红点,那么,可增加
个行对.考虑最后两行:若第1列还有红点,那么,有红点的这一行不能再有其他的红点.如第1列还有2个红点,这时能增加9个行对,6×6方格表中共有11+9=20个行对;如第1 列还有1个红点,不妨设第1列第5行的小方格有红点,这时即使第6行除第1列外的其他小方格都有红点,那么,可增加![]() 个行对,6×6方格表中共有11+14=25个行对;如第1列没有其他的红点,那么,在最后两行中最多还有两个行对,这两个行对占去了两列,在余下的三列中,每列最多有1个红点,于是,可增加行对2×5+3×2=16个,这时,6×6方格表中最多有11+16=27个行对.这说明27是可能的行对总数的最大值.
个行对,6×6方格表中共有11+14=25个行对;如第1列没有其他的红点,那么,在最后两行中最多还有两个行对,这两个行对占去了两列,在余下的三列中,每列最多有1个红点,于是,可增加行对2×5+3×2=16个,这时,6×6方格表中最多有11+16=27个行对.这说明27是可能的行对总数的最大值.
设第i列的红点数为![]() ,
,
且![]() .则所有行对的总数
.则所有行对的总数![]() ,即
,即![]() .
.
由柯西不等式有![]() .
.
所以,![]() .
.
解得![]() .
.
由k为正整数知k≤21.这说明6×6方格表中红点个数最多为21个.
又当n≤5时,方格表中红点总数不大于4×5=20个.这说明n的最小值不小于7.
综上,该代表队至少有7名选手


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
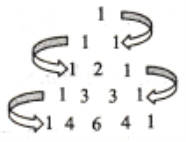
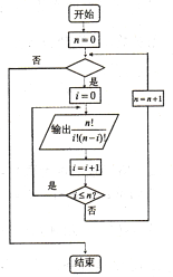
【题目】杨辉三角是二项式系数在三角形中的一种几何排列,是中国古代数学的杰出研究成果之一.在欧洲,左下图叫帕斯卡三角形,帕斯卡在1654年发现的这一规律,比杨辉要迟393年,比贾宪迟600年.某大学生要设计一个程序框图,按右下图标注的顺序将表上的数字输出,若第5次输出数“1”后结束程序,则空白判断框内应填入的条件为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代中的“礼、乐、射、御、书、数”合称“六艺”.“礼”,主要指德育;“乐”,主要指美育;“射”和“御”,就是体育和劳动;“书”,指各种历史文化知识;“数”,数学.某校国学社团开展“六艺”课程讲座活动,每艺安排一节,连排六节,一天课程讲座排课有如下要求:“数”必须排在前三节,且“射”和“御”两门课程相邻排课,则“六艺”课程讲座不同排课顺序共有( )
A. ![]() 种 B.
种 B. ![]() 种 C.
种 C. ![]() 种 D.
种 D. ![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年春节期间,某超市准备举办一次有奖促销活动,若顾客一次消费达到400元则可参加一次抽奖活动,超市设计了两种抽奖方案.
方案一:一个不透明的盒子中装有30个质地均匀且大小相同的小球,其中10个红球,20个白球,搅拌均匀后,顾客从中随机抽取一个球,若抽到红球则顾客获得60元的返金券,若抽到白球则获得20元的返金券,且顾客有放回地抽取3次.
方案二:一个不透明的盒子中装有30个质地均匀且大小相同的小球,其中10个红球,20个白球,搅拌均匀后,顾客从中随机抽取一个球,若抽到红球则顾客获得80元的返金券,若抽到白球则未中奖,且顾客有放回地抽取3次.
(1)现有两位顾客均获得抽奖机会,且都按方案一抽奖,试求这两位顾客均获得180元返金券的概率;
(2)若某顾客获得抽奖机会.
①试分别计算他选择两种抽奖方案最终获得返金券的数学期望;
②为了吸引顾客消费,让顾客获得更多金额的返金券,该超市应选择哪一种抽奖方案进行促销活动?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 在左、右焦点分别为
在左、右焦点分别为![]() ,
,![]() ,动点
,动点![]() 在椭圆
在椭圆![]() 上,
上,![]() 的周长为6,且面积的最大值为
的周长为6,且面积的最大值为![]() .
.
(1)求![]() 的方程;
的方程;
(2)设直线![]() 与
与![]() 的另一个交点为
的另一个交点为![]() ,过
,过![]() ,
,![]() 分别作直线
分别作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,
,![]() ,
,![]() 与
与![]() 轴的交点为
轴的交点为![]() .若
.若![]() ,
,![]() ,
,![]() 的面积成等差数列,求直线
的面积成等差数列,求直线![]() 斜率的取值范围.
斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市教学研究室为了对今后所出试题的难度有更好的把握,提高命题质量,对该市高三理科数学试卷的得分情况进行了调研.从全市参加考试的理科考生中随机抽取了100名考生的数学成绩(满分150分),将数据分成9组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并整理得到如图所示的频率分布直方图.用统计的方法得到样本标准差
,并整理得到如图所示的频率分布直方图.用统计的方法得到样本标准差![]() ,以频率值作为概率估计值.
,以频率值作为概率估计值.

(Ⅰ)根据频率分布直方图,求抽取的100名理科考生数学成绩的平均分![]() 及众数
及众数![]() ;
;
(Ⅱ)用频率估计概率,从该市所有高三理科考生的数学成绩中随机抽取3个,记理科数学成绩位于区间![]() 内的个数为
内的个数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(Ⅲ)从该市高三理科数学考试成绩中任意抽取一份,记其成绩为![]() ,依据以下不等式评判(
,依据以下不等式评判(![]() 表示对应事件的概率):
表示对应事件的概率):
①![]() ,②
,②![]() ,
,
③![]() ,其中
,其中![]() .
.
评判规则:若至少满足以上两个不等式,则给予这套试卷好评,否则差评.试问:这套试卷得到好评还是差评?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次篮球投篮测试中,记分规则如下(满分为![]() 分):①每人可投篮
分):①每人可投篮![]() 次,每投中一次记
次,每投中一次记![]() 分;②若连续两次投中加
分;②若连续两次投中加![]() 分,连续三次投中加
分,连续三次投中加![]() 分,连续四次投中加
分,连续四次投中加![]() 分,以此类推,…,七次都投中加
分,以此类推,…,七次都投中加![]() 分.假设某同学每次投中的概率为
分.假设某同学每次投中的概率为![]() ,各次投篮相互独立,则:(1)该同学在测试中得
,各次投篮相互独立,则:(1)该同学在测试中得![]() 分的概率为______;(2)该同学在测试中得
分的概率为______;(2)该同学在测试中得![]() 分的概率为______..
分的概率为______..
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com