科目：高中数学 来源： 题型：解答题
如图所示，n台机器人M1，M2，……，Mn位于一条直线上，检测台M在线段M1 Mn上，n台机器人需把各自生产的零件送交M处进行检测，送检程序设定：当Mi把零件送达M处时，Mi+1即刻自动出发送检（i=1,2,……,n-1）已知Mi的送检速度为V(V>0), 且
记
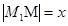，n台机器人送检时间总和为f(x).
 |
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
对于函数f(x)若存在x0∈R，f(x0)＝x0成立，则称x0为f(x)的不动点．已知f(x)＝ax2＋(b＋1)x＋b－1(a≠0)．
(1)当a＝1，b＝－2时，求函数f(x)的不动点；
(2)若对任意实数b，函数f(x)恒有两个相异的不动点，求a的取值范围；
(3)在(2)的条件下，若y＝f(x)图象上A，B两点的横坐标是函数f(x)的不动点，且A，B两点关于直线y＝kx＋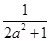
对称，求b的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
某加油站拟造如图所示的铁皮储油罐（不计厚度，长度单位：米），其中储油罐的中间为圆柱形，左右两端均为半球形，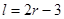
（
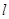为圆柱的高，
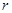为球的半径，
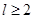）.假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为
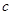千元，半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为
千元.
（1）写出关于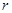的函数表达式，并求该函数的定义域；
（2）求该储油罐的建造费用最小时的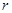的值.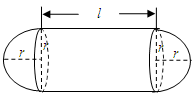
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
(2014·孝感模拟)已知定义在区间[0,2]上的两个函数f(x)和g(x),其中f(x)=-x2+2ax+1+a2,g(x)=x-
+
.
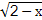(1)求函数f(x)的最小值.
(2)对于?x1,x2∈[0,2],f(x1)>g(x2)恒成立,求实数a的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
湛江为建设国家卫生城市，现计划在相距20 km的赤坎区（记为A）霞山区（记为B）两城区外以AB为直径的半圆弧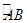
上选择一点C建造垃圾处理厂，其对市区的影响度与所选地
点到市区的距离有关，对赤坎区和霞山区的总影响度为两市区的影响度之和，记C点到赤坎区的距离为x km，建在C处的垃圾处理厂对两市区的总影响度为y.统计调查表明：垃圾处理厂对赤坎区的影响度与所选地点到赤坎区的距离的平方成反比，比例系数为4；对霞山区的影响度与所选地点到霞山区的距离的平方成反比，比例系数为k.当垃圾处理厂建在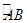的中点时，对两市区的总影响度为0.065.
(1)将y表示成x的函数；
(2)讨论(1)中函数的单调性，并判断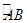上是否存在一点，使建在此处的垃圾处理厂对城A和城B的总影响度最小？若存在，求出该点到赤坎区的距离；若不存在，说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
为了保护环境，某工厂在国家的号召下，把废弃物回收转化为某种产品，经测算，处理成本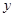
（万元）与处理量
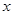（吨）之间的函数关系可近似的表示为：
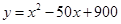，且每处理一吨废弃物可得价值为
万元的某种产品，同时获得国家补贴万元．
（1）当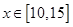
时，判断该项举措能否获利？如果能获利，求出最大利润；
如果不能获利，请求出国家最少补贴多少万元，该工厂才不会亏损？
（2）当处理量为多少吨时，每吨的平均处理成本最少？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
都有|f(x)|≤1成立，试求a的取值范围．
（
为实常数）．
，求函数
的单调区间；
上的最小值为
，求
)，试确定m的值，并求满足条件f(2－a)>f(a－1)的实数a的取值范围．