
【题目】下表是最近十届奥运会的年份、届别、主办国,以及主办国在上届获得的金牌数、当届
获得的金牌数的统计数据:
年份 | 1972 | 1976 | 1980 | 1984 | 1988 | 1992 | 1996 | 2000 | 2004 | 2008 |
届别 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
主办国家 | 联邦 德国 | 加拿大 | 苏联 | 美国 | 韩国 | 西班牙 | 美国 | 澳大 利亚 | 希腊 | 中国 |
上届金牌数 | 5 | 0 | 49 | 未参加 | 6 | 1 | 37 | 9 | 4 | 32 |
当界金牌数 | 13 | 0 | 80 | 83 | 12 | 13 | 44 | 16 | 6 | 51 |
某体育爱好组织,利用上表研究所获金牌数与主办奥运会之间的关系,
(1)求出主办国在上届所获金牌数(设为![]() )与在当届所获金牌数(设为
)与在当届所获金牌数(设为![]() )之间的线性回归方程
)之间的线性回归方程
![]() 其中
其中![]()
(2)在2008年第29届北京奥运会上日本获得9块金牌,则据此线性回归方程估计在2020 年第 32 届东
京奥运会上日本将获得的金牌数为(所有金牌数精确到整数)
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρcosθ=4.
(Ⅰ)M为曲线C1上的动点,点P在线段OM上,且满足|OM||OP|=16,求点P的轨迹C2的直角坐标方程;
(Ⅱ)设点A的极坐标为(2, ![]() ),点B在曲线C2上,求△OAB面积的最大值.
),点B在曲线C2上,求△OAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
(Ⅰ)求六月份这种酸奶一天的需求量X(单位:瓶)的分布列;
(Ⅱ)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量n(单位:瓶)为多少时,Y的数学期望达到最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)(x∈R)满足f(x)=f(2-x),且对任意的x1,x2∈(-∞,1](x1≠x2)有(x1-x2)(f(x1)-f(x2))<0.则( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对一个样本容量为100的数据分组,各组的频数如表:
区间 | [17,19) | [19,21) | [21,23) | [23,25) | [25,27) | [27,29) | [29,31) | [31,33] |
频数 | 1 | 1 | 3 | 3 | 18 | 16 | 28 | 30 |
估计小于29的数据大约占总体的( )
A. 16% B. 40% C. 42% D. 58%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,其中AD∥BC,AB⊥AD,AB=AD= ![]() BC,
BC, ![]() =
= ![]()
![]() .
. 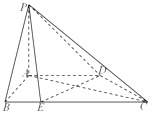
(1)求证:DE⊥平面PAC;
(2)若直线PE与平面PAC所成角的正弦值为 ![]() ,求二面角A﹣PC﹣D的平面角的余弦值.
,求二面角A﹣PC﹣D的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的参数方程是 ![]() (θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,A、B的极坐标分别为A﹣(2,0)、B(﹣1,
(θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,A、B的极坐标分别为A﹣(2,0)、B(﹣1, ![]() )
)
(1)求直线AB的直角坐标方程;
(2)在曲线C上求一点M,使点M到AB的距离最大,并求出些最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:
①圆![]() 与直线
与直线![]() 相交,所得弦长为
相交,所得弦长为![]() ;
;
②直线![]() 与圆
与圆![]() 恒有公共点;
恒有公共点;
③若棱长为![]() 的正方体的顶点都在同一球面上,则该球的表面积为
的正方体的顶点都在同一球面上,则该球的表面积为![]() ;
;
④若棱长为![]() 的正四面体的顶点都在同一球面上,则该球的体积为
的正四面体的顶点都在同一球面上,则该球的体积为![]() .
.
其中,正确命题的序号为__________.(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域为R的函数f(x)满足:对于任意的实数x,y都有f(x+y)=f(x)+f(y)成立,且当x<0时,f(x)>0恒成立,且nf(x)=f(nx).(n是一个给定的正整数).
(1)判断函数f(x)的奇偶性,并证明你的结论;
(2)证明f(x)为减函数;若函数f(x)在[-2,5]上总有f(x)≤10成立,试确定f(1)应满足的条件;
(3)当a<0时,解关于x的不等式![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com