
【题目】已知椭圆 ![]() +y2=1(m>1)和双曲线
+y2=1(m>1)和双曲线 ![]() ﹣y2=1(n>0)有相同的焦点F1 , F2 , P是它们的一个交点,则△F1PF2的形状是( )
﹣y2=1(n>0)有相同的焦点F1 , F2 , P是它们的一个交点,则△F1PF2的形状是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.随m,n的变化而变化
【答案】B
【解析】解:由题意设两个圆锥曲线的焦距为2c,椭圆的长轴长2 ![]() , 双曲线的实轴长为2
, 双曲线的实轴长为2 ![]() ,
,
不妨令P在双曲线的右支上,
由双曲线的定义|PF1|﹣|PF2|=2 ![]() ,①
,①
由椭圆的定义|PF1|+|PF2|=2 ![]() ,②
,②
∵m﹣n=2,∴n=m﹣2,
①2+②2得|PF1|2+|PF2|2=2(m+n),
又∵椭圆 ![]() +y2=1(m>1)和双曲线
+y2=1(m>1)和双曲线 ![]() ﹣y2=1(n>0)有相同的焦点F1 , F2 ,
﹣y2=1(n>0)有相同的焦点F1 , F2 ,
∴m﹣1=n+1,∴m﹣n=2,
∴|PF1|2+|PF2|2=2(m+n)=4m﹣4,
|F1F2|2=(2 ![]() )2=4m﹣4,
)2=4m﹣4,
∴|PF1|2+|PF2|2=|F1F2|,
则△F1PF2的形状是直角三角形
故选:B.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,以E的四个顶点为顶点的四边形的面积为4
,以E的四个顶点为顶点的四边形的面积为4 ![]() . (Ⅰ)求椭圆E的方程;
. (Ⅰ)求椭圆E的方程;
(Ⅱ)设A,B分别为椭圆E的左、右顶点,P是直线x=4上不同于点(4,0)的任意一点,若直线AP,BP分别与椭圆相交于异于A,B的点M、N,试探究,点B是否在以MN为直径的圆内?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知OPQ是半径为 ![]() 圆心角为
圆心角为 ![]() 的扇形,C是该扇形弧上的动点,ABCD是扇形的内接矩形,记∠BOC为α.
的扇形,C是该扇形弧上的动点,ABCD是扇形的内接矩形,记∠BOC为α. 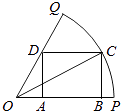
(Ⅰ)若Rt△CBO的周长为 ![]() ,求
,求 ![]() 的值.
的值.
(Ⅱ)求 ![]() 的最大值,并求此时α的值.
的最大值,并求此时α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(1﹣x)+loga(x+3)(a>0,且a≠1)
(1)求函数f(x)的定义域和值域;
(2)若函数 f(x)有最小值为﹣2,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
参考公式:b= 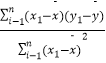 =
= 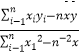 .
.
(1)画出散点图;
(2)求回归直线方程;
(3)试预测广告费支出为10百万元时,销售额多大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com