
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若对任意![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,
时, ![]() 在
在![]() 为增函数,
为增函数, ![]() 在
在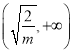 为减函数;当
为减函数;当![]() 时,
时, ![]() 在
在![]() 为增函数,在
为增函数,在 为减函数;(2)
为减函数;(2)![]() .
.
【解析】试题分析:(1)先求出函数导数![]() ,根据导函数符号的判定来下结论,因为此时导函数分子带参数无法确定符号,故进行讨论,通常根据参数大于0,等于0,小于0一一讨论定号即可得出单调性,但要注意定义域的限制;(2)恒成立问题通常转化最值问题求解,求参数取值范围我们一般会优先考虑参数分离形成新函数求最值,本题即可
,根据导函数符号的判定来下结论,因为此时导函数分子带参数无法确定符号,故进行讨论,通常根据参数大于0,等于0,小于0一一讨论定号即可得出单调性,但要注意定义域的限制;(2)恒成立问题通常转化最值问题求解,求参数取值范围我们一般会优先考虑参数分离形成新函数求最值,本题即可![]() 在
在![]() 上恒成立, 即
上恒成立, 即![]() 在
在![]() 上恒成立。,接下来分析函数
上恒成立。,接下来分析函数 ![]() 在
在![]() 上的最大值即可得出结论
上的最大值即可得出结论
解析:(1)由题知: ![]() ,
,
当m≤0时, ![]() >0在x∈(0,+∞)时恒成立,
>0在x∈(0,+∞)时恒成立,
∴f(x)在(0,+∞)上是增函数.
当m>0时, 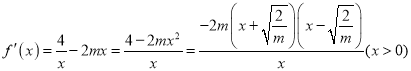 ,
,
令f′(x)>0,则![]() ;令f′(x)<0, 则
;令f′(x)<0, 则![]() .
.
∴f(x)在![]() 为增函数,f(x)在
为增函数,f(x)在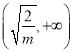 为减函数.
为减函数.
(2)法一:由题知: ![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立。
上恒成立。
令![]() ,所以
,所以 ![]()
令g′(x)>0,则![]() ;令g′(x)<0,则
;令g′(x)<0,则![]() .
.
∴g(x)在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
∴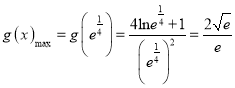 ,∴
,∴![]() .
.
法二:要使f(x) ≤0恒成立,只需![]() ,
,
(1)当m≤0时,f(x)在[1,e]上单调递增,所以 ![]() ,
,
即![]() ,这与m≤0矛盾,此时不成立.
,这与m≤0矛盾,此时不成立.
(2)当m>0时,
① 若![]() 即
即![]() 时,f(x)在[1,e]上单调递增,
时,f(x)在[1,e]上单调递增,
所以![]() ,即
,即![]() , 这与
, 这与![]() 矛盾,此时不成立.
矛盾,此时不成立.
②若1< ![]() 即
即![]() 时,f(x)在
时,f(x)在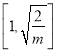 上单调递增,在
上单调递增,在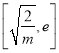 上单调递减 .
上单调递减 .
所以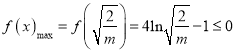 即
即![]() ,
,
解得 ![]() ,又因为
,又因为![]() ,所以
,所以 ![]() ,
,
③![]() 即m
即m![]() 2时,f(x)在
2时,f(x)在![]() 递减,则
递减,则![]() ,
,
∴![]() 又因为
又因为![]() ,所以m
,所以m![]() 2,综上
2,综上![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx。
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求证:当x>0时,f(x)≥l-![]() ;
;
(3)若x-1>alnx对任意x>1恒成立,求实数a的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关系式中正确的是( )
A. sin11°<cos10°<sin168° B. sin168°<sin11°<cos10°
C. sin11°<sin168°<cos10° D. sin168°<cos10°<sin11°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆的方程;
(2)设直线![]() 与椭圆相交于
与椭圆相交于![]() ,
, ![]() 两点,
两点, ![]() ,
, ![]() 分别为线段
分别为线段![]() ,
, ![]() 的中点,若坐标原点
的中点,若坐标原点![]() 在以
在以![]() 为直径的圆上,求
为直径的圆上,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,正方形![]() 所在的平面与正三角形ABC所在的平面互相垂直,
所在的平面与正三角形ABC所在的平面互相垂直, ![]() ,且
,且![]() ,
, ![]() 是
是![]() 的中点.
的中点.
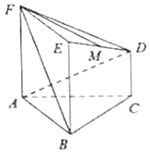
(1)求证: ![]() ∥平面
∥平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥中,SA=SB=AB=BC=CA=6,且侧面ASB⊥底面ABC,则三棱锥S-ABC外接球的表面积为( )

A. 60π B. 56π C. 52π D. 48π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,平面四边形ABCD中AD∥BC,∠BAD为二面角B﹣PA﹣D一个平面角. 
(1)若四边形ABCD是菱形,求证:BD⊥平面PAC;
(2)若四边形ABCD是梯形,且平面PAB∩平面PCD=l,问:直线l能否与平面ABCD平行?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com