练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    平面向量的集合A到A的映射f(
    x
    )=
    x
    -(
    x
    •
    a
    )•
    a
    ，其中
    a
    为常向量，若f满足f(
    x
    )•f(
    y
    )=
    x
    •
    y
    对任意
    x
    ，
    y
    ∈A    成立，则
    a
    的坐标可以是（　　）
    分析：令
    y
    =
    x
    ，可得f(
    x
    )•f(
    x
    )    =[
    x
    -(
    x
    •
    a
    )•
    a
    ]2    =
    x
    2    -2(
    x
    •
    a
    )    2    +[(
    x
    •
    a
    )
    a
    ]    2    =
    x
    2    ，变形可解得|
    a
    |=0    ，或|
    a
    |=
    		2
    ，验证选项可得．
    解答：解：令
    y
    =
    x
    ，代入已知可得f(
    x
    )•f(
    x
    )=
    x
    •
    x
    ，
    又f(
    x
    )=
    x
    -(
    x
    •
    a
    )•
    a
    ，
    ∴f(
    x
    )•f(
    x
    )    =[
    x
    -(
    x
    •
    a
    )•
    a
    ]2    =
    x
    2    -2(
    x
    •
    a
    )    2    +[(
    x
    •
    a
    )
    a
    ]    2    =
    x
    2    ，
    变形可得-2(
    x
    •
    a
    )    2    +[(
    x
    •
    a
    )
    a
    ]    2    =0，即(
    x
    •
    a
    )2(-2+
    a
    2    )    =0
    ∴
    a
    =
    0
    ，或
    a
    2    =2，即|
    a
    |=0    ，或|
    a
    |=
    		2

    验证选项可得B符合题意，
    故选B
    点评：本题考查平面向量数量积的运算，涉及映射的知识和抽象函数的赋值法，属中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    平面向量的集合A到A的映射f由f（
    x
    ）=
    x
    -2(
    x
    •
    a
    )  
    a
    确定，其中
    a
    为常向量．若映射f满足f(
    x
    ) •f(
    y
    ) =
    x
    • 
    y
    对
    x
    ，
    y
    ∈A    恒成立，则
    a
    的坐标不可能是（　　）
    A、（0，0）
    B、（-
    		2
    4
    ，
    		2
    4
    ）
    C、（-
    		2
    2
    ，
    		2
    2
    ）
    D、（-
    1
    2
    ，
    		3
    2
    ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    平面向量的集合A到A的映射f由f(x)=x-2(x·a)a确定,其中a为常向量.若映射f满足f(x)·f(y)=x·y对任意x、y∈A恒成立,则a的坐标可能是

    A.(,)                             B.(,)

    C.(,)                                D.(,)

    查看答案和解析>>

    科目：高中数学 来源：2012年河北省衡水中学高考数学信息卷5（理科）（解析版） 题型：选择题

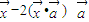    平面向量的集合A到A的映射f由f（）=确定，其中为常向量．若映射f满足对恒成立，则的坐标不可能是（ ）
    A．（0，0）
    B．（-，）
    C．（-，）
    D．（-，）

    查看答案和解析>>

    科目：高中数学 来源：2009-2010学年湖北省“黄冈中学、黄石二中、华师一附中、荆州中学、孝感高中、襄樊四中、襄樊五中、鄂南高中”八校高三第一次联考数学试卷（理科）（解析版） 题型：选择题

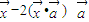    平面向量的集合A到A的映射f由f（）=确定，其中为常向量．若映射f满足对恒成立，则的坐标不可能是（ ）
    A．（0，0）
    B．（-，）
    C．（-，）
    D．（-，）

    查看答案和解析>>

    同步练习册答案