
【题目】已知函数![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线与坐标轴围成的三角形的面积;
处的切线与坐标轴围成的三角形的面积;
(Ⅱ)若![]() 在区间
在区间![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】试题分析:(I)当a=1时,f(x)=ex+x-1,根据导数的几何意义可求得在点(1,f(1))处的切线的斜率,再由点斜式即可得切线方程,分别求出切线与x轴、y轴的交点A、B,利用直角三角形的面积公式即可求得;
(II)将f(x)≥x2在(0,1)上恒成立利用参变量分离法转化为![]() 在(0,1)上恒成立,再利用导数研究不等式右边的函数的单调性,从而求出函数的最大值,即可求出a的取值范围.
在(0,1)上恒成立,再利用导数研究不等式右边的函数的单调性,从而求出函数的最大值,即可求出a的取值范围.
试题解析:
(Ⅰ)∵当![]() 时,
时, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
∴函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,
,
即![]() .
.
设切线与![]() 轴的交点分别为
轴的交点分别为![]() ,
,
令![]() 得,
得, ![]() ,令
,令![]() 得,
得, ![]() ,
,
∴![]() ,
, ![]() ,∴
,∴![]() ,
,
∴函数![]() 在点
在点![]() 处的切线与坐标轴围成的三角形的面积为
处的切线与坐标轴围成的三角形的面积为![]() .
.
(Ⅱ)由![]() 得,
得, ![]() .
.
令![]() ,
,
则![]()
![]() ,
,
令![]() ,则
,则![]() .
.
∵![]() ,∴
,∴![]() ,
, ![]() 在区间
在区间![]() 上为减函数,∴
上为减函数,∴![]() .
.
又![]() ,
, ![]() ,∴
,∴![]() ,
,
∴![]() 在区间
在区间![]() 上为增函数,
上为增函数, ![]() ,
,
因此只需![]() 即可满足题意.
即可满足题意.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】2019年春节期间,当红影视明星翟天临“不知”“知网”学术不端事件在全国闹得沸沸扬扬,引发了网友对亚洲最大电影学府北京电影学院乃至整个中国学术界高等教育乱象的反思.为进一步端正学风,打击学术造假行为,教育部日前公布的2019年部门预算中透露,2019年教育部拟抽检博士学位论文约![]() 篇,预算为
篇,预算为![]() 万元.国务院学位委员会、教育部2014年印发的《博士硕士学位论文抽检办法》通知中规定:每篇抽检的学位论文送
万元.国务院学位委员会、教育部2014年印发的《博士硕士学位论文抽检办法》通知中规定:每篇抽检的学位论文送![]() 位同行专家进行评议,
位同行专家进行评议,![]() 位专家中有
位专家中有![]() 位以上(含
位以上(含![]() 位)专家评议意见为“不合格”的学位论文,将认定为“存在问题学位论文”;有且只有
位)专家评议意见为“不合格”的学位论文,将认定为“存在问题学位论文”;有且只有![]() 位专家评议意见为“不合格”的学位论文,将再送
位专家评议意见为“不合格”的学位论文,将再送![]() 位同行专家进行复评.
位同行专家进行复评. ![]() 位复评专家中有
位复评专家中有![]() 位以上(含
位以上(含![]() 位)专家评议意见为“不合格”的学位论文,将认定为“存在问题学位论文”设每篇学位论文被每位专家评议为“不合格”的概率均为
位)专家评议意见为“不合格”的学位论文,将认定为“存在问题学位论文”设每篇学位论文被每位专家评议为“不合格”的概率均为![]() 且各篇学位论文是否被评议为“不合格”相互独立.
且各篇学位论文是否被评议为“不合格”相互独立.
(1)相关部门随机地抽查了![]() 位博士硕士的论文,每人一篇,抽检是否合格,抽检得到的部分数据如下表所示:
位博士硕士的论文,每人一篇,抽检是否合格,抽检得到的部分数据如下表所示:
合格 | 不合格 | |
博士学位论文 |
|
|
硕士学位论文 |
|
|
通过计算说明是否有![]() 的把握认为论文是否合格与作者的学位高低有关系?
的把握认为论文是否合格与作者的学位高低有关系?
(2)若![]() ,记一篇抽检的学位论文被认定为“存在问题学位论文”的概率为
,记一篇抽检的学位论文被认定为“存在问题学位论文”的概率为![]() ,求
,求![]() 的值;
的值;
(3)若拟定每篇抽检论文不需要复评的评审费用为![]() 元,需要复评的评审费用为
元,需要复评的评审费用为![]() 元;除评审费外,其他费用总计为
元;除评审费外,其他费用总计为![]() 万元现以此方案实施,且抽检论文为
万元现以此方案实施,且抽检论文为![]() 篇,问是否会超过预算?并说明理由.
篇,问是否会超过预算?并说明理由.
临界值表:
|
|
|
|
|
|
|
|
|
|
|
|
参考公式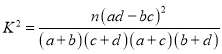 ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.根据该折线图,下列结论错误的是( )
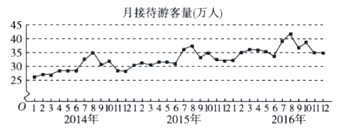
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() 的最小值为-2,
的最小值为-2,![]() 的图象的相邻两条对称轴之间的距离为
的图象的相邻两条对称轴之间的距离为![]() ,
,![]() 的图象过点
的图象过点![]() .
.
(1)求函数![]() 的解析式和单调递增区间;
的解析式和单调递增区间;
(2)若![]() 函数
函数![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体有8个不同顶点,现任意选择其中4个不同顶点,然后将它们两两相连,可组成平面图形成空间几何体.在组成的空间几何体中,可以是下列空间几何体中的________.(写出所有正确结论的编号)
①每个面都是直角三角形的四面体;
②每个面都是等边三角形的四面体;
③每个面都是全等的直角三角形的四面体;
④有三个面为等腰直角三角形,有一个面为等边三角形的四面体.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,曲线C的参数方程为![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为![]() .
.
(1)若a=1,求C与l的交点坐标;
(2)若C上的点到l的距离的最大值为![]() ,求a.
,求a.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com