
【题目】已知![]() ,
,![]() 。
。
(1)当![]() 时,求f(x)的最大值。
时,求f(x)的最大值。
(2)若函数f(x)的零点个数为2个,求![]() 的取值范围。
的取值范围。
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)求出![]() ,再求出
,再求出![]() ,利用
,利用![]() 的正负判断
的正负判断![]() 的单调性,从而判断
的单调性,从而判断![]() 的正负,从而判断
的正负,从而判断![]() 的单调性,进而求得函数
的单调性,进而求得函数![]() 的最值。
的最值。
(2)求出![]() ,再求出
,再求出![]() ,求得函数
,求得函数![]() 单调性,对参数
单调性,对参数![]() 的范围分类讨论,求得函数的最值,结合函数
的范围分类讨论,求得函数的最值,结合函数![]() 的单调性,从而判断函数
的单调性,从而判断函数![]() 的零点个数。
的零点个数。
解:(1)当![]() 时,
时,
![]()
![]() .因为
.因为![]() 时,
时,
![]()
所以![]() 在
在![]() 上为减函数.(
上为减函数.(![]() 递减说明言之有理即可)
递减说明言之有理即可)
又![]() ,所以当
,所以当![]() 时,
时,![]() ,函数
,函数![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减;故
单调递减;故![]() .
.
(2)![]() ,
,![]() ,
,
当![]() ,且
,且![]() 时,
时,![]() .
.
所以![]() 在
在![]() 上为减函数
上为减函数
![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,故存在
,故存在![]() 使得
使得
![]() ,且有
,且有![]() 在
在![]() 上递增,
上递增,
在![]() 递减,
递减,![]() .
.
①当![]() 时由(1)知只有唯一零点
时由(1)知只有唯一零点
②当![]() 时,
时,![]() 即有
即有![]() ,
,
此时有2个零点
③当![]() 时,
时,![]() ,
,
![]()
![]()
又有![]() ,故
,故![]() .
.
令![]() ,
,![]()
![]() ,故
,故![]() 在定义域内单调递增.
在定义域内单调递增.
而![]() ,故
,故![]() ,于是
,于是![]() ,所以
,所以![]() 时不存在零点.
时不存在零点.
综上:函数![]() 的零点个数为2个,
的零点个数为2个,![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知正四面体ABCD的棱长为2,球O与四面体的面ABC和面DBC都相切,其切点分别在△ABC和△DBC内(含边界),且球O与棱AD相切.
(1)证明:球O的球心在棱AD的中垂面上;
(2)求球O的半径的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《易经》是中国传统文化中的精髓,如图是易经八卦(含乾、坤、巽、震、坎、离、艮、兑八卦),每一卦由三根线组成("![]() "表示一根阳线,"
"表示一根阳线,"![]() "表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有两根阳线,四根阴线的概率为_______.
"表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有两根阳线,四根阴线的概率为_______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2013年5月,华人数学家张益唐的论文《素数间的有界距离》在《数学年刊》上发表,破解了困扰数学界长达一个多世纪的难题,证明了孪生素数猜想的弱化形式,即发现存在无穷多差小于7000万的素数对.这是第一次有人证明存在无穷多组间距小于定值的素数对.孪生素数猜想是希尔伯特在1900年提出的23个问题中的第8个,可以这样描述:存在无穷多个素数![]() ,使得
,使得![]() 是素数,素数对
是素数,素数对![]() 称为孪生素数.在不超过16的素数中任意取出不同的两个,则可组成孪生素数的概率为( )
称为孪生素数.在不超过16的素数中任意取出不同的两个,则可组成孪生素数的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C:![]() +y2=1(a>1)的上顶点为A,右焦点为F,直线AF与圆M:x2+y2-6x-2y+7=0相切.
+y2=1(a>1)的上顶点为A,右焦点为F,直线AF与圆M:x2+y2-6x-2y+7=0相切.
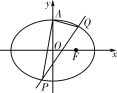
(1)求椭圆C的方程;
(2)若不过点A的动直线l与椭圆C相交于P,Q两点,且![]() =0,求证:直线l过定点,并求出该定点N的坐标.
=0,求证:直线l过定点,并求出该定点N的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com