
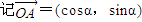 ,
,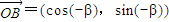 ,用两种方法计算
,用两种方法计算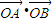 后,利用等量代换可以得到的等式是 .
后,利用等量代换可以得到的等式是 .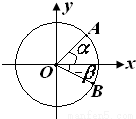
科目:高中数学 来源: 题型:
 (2009•黄浦区一模)如图所示,点A、B是单位圆(圆心在原点,半径为1的圆)上两点,OA、OB与x轴正半轴所成的角分别为α和-β.记
(2009•黄浦区一模)如图所示,点A、B是单位圆(圆心在原点,半径为1的圆)上两点,OA、OB与x轴正半轴所成的角分别为α和-β.记| OA |
| OB |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源:2010年上海市黄浦区高考数学一模试卷(理科)(解析版) 题型:解答题
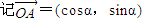 ,
,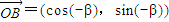 ,用两种方法计算
,用两种方法计算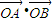 后,利用等量代换可以得到的等式是 .
后,利用等量代换可以得到的等式是 .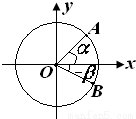
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com