
【题目】已知a,b,c分别是△ABC的三个内角A,B,C所对的边,且满足(2b﹣a)cosC=ccosA. (Ⅰ)求角C的大小;
(Ⅱ)设y=﹣4 ![]() sin2
sin2 ![]() +2sin(C﹣B),求y的最大值并判断当y取得最大值时△ABC的形状.
+2sin(C﹣B),求y的最大值并判断当y取得最大值时△ABC的形状.
【答案】解:(I)∵(2b﹣a)cosC=ccosA, 由正弦定理可得:(2sinB﹣sinA)cosC=sinCcosA,
化为:2sinBcosC=sin(C+A)=sinB,
∵sinB≠0,∴cosC= ![]() ,
,
∵C∈(0,π),∴C= ![]() .
.
(II)y=﹣4 ![]() sin2
sin2![]() +2sin(C﹣B)=
+2sin(C﹣B)= ![]() (1﹣cosA)+2sin
(1﹣cosA)+2sin ![]() =sinA+
=sinA+ ![]() cosA﹣2
cosA﹣2 ![]() =2
=2 ![]() ﹣2
﹣2 ![]() ,
,
∵A∈ ![]() ,∴
,∴ ![]() ∈
∈ ![]() ,
,
∴当A+ ![]() =
= ![]() ,即A=
,即A= ![]() 时,y确定最大值2﹣2
时,y确定最大值2﹣2 ![]() ,此时B=
,此时B= ![]() ,
,
因此△ABC为直角三角形.
【解析】(I)由(2b﹣a)cosC=ccosA,由正弦定理可得:(2sinB﹣sinA)cosC=sinCcosA,利用和差关系化简可得:cosC= ![]() ,即可得出C. (II)利用倍角公式、和差公式可得:y=2
,即可得出C. (II)利用倍角公式、和差公式可得:y=2 ![]() ﹣2
﹣2 ![]() ,再利用三角函数的单调性及其最值可得A,再利用三角形内角和定理即可得出.
,再利用三角函数的单调性及其最值可得A,再利用三角形内角和定理即可得出.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,AB∥CD,∠BAD=90°,AD= ![]() ,DC=2AB=2,E为BC中点.
,DC=2AB=2,E为BC中点. 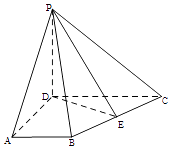
(1)求证:平面PBC⊥平面PDE
(2)线段PC上是否存在一点F,使PA∥平面BDF?若存在,求 ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在斜三棱柱ABC﹣A1B1C1中,∠BAC=90°,BC1⊥AC,则C1在面ABC上的射影H必在( ) 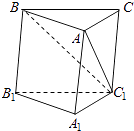
A.直线AB上
B.直线BC上
C.直线CA上
D.△ABC内部
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元). (Ⅰ)将y表示为x的函数:
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,设右焦点为
,设右焦点为![]() ,过原点
,过原点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,线段
,线段![]() 的中点为
的中点为![]() ,且
,且![]() .
.
(1)求弦![]() 的长;
的长;
(2)当直线![]() 的斜率
的斜率![]() ,且直线
,且直线![]() 时,
时, ![]() 交椭圆于
交椭圆于![]() ,若点
,若点![]() 在第一象限,求证:直线
在第一象限,求证:直线![]() 与
与![]() 轴围成一个等腰三角形.
轴围成一个等腰三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x∈[1,2],x2﹣a≥0;命题q:x0∈R,使得 ![]() +(a﹣1)x0+1<0.若“p或q”为真,“p且q”为假,则实数a的取值范围
+(a﹣1)x0+1<0.若“p或q”为真,“p且q”为假,则实数a的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c. (Ⅰ)求C;
(Ⅱ)若c= ![]() ,△ABC的面积为
,△ABC的面积为 ![]() ,求△ABC的周长.
,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x2+x+m)ex(其中m∈R,e为自然对数的底数).若在x=﹣3处函数f (x)有极大值,则函数f (x)的极小值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com