
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上.
上.
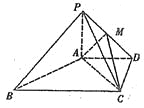
(1)求证:![]() 平面
平面![]() ;
;
(2)若二面角![]() 的大小为
的大小为![]() ,试确定点
,试确定点![]() 的位置.
的位置.
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】山东新旧动能转换综合试验区是党的十九大后获批的首个区域性国家发展战略,也是中国第一个以新旧动能转换为主题的区域发展战略.泰安某高新技术企业决定抓住发展机遇,加快企业发展.已知该企业的年固定成本为500万元,每生产设备![]() 台,需另投入成本
台,需另投入成本![]() 万元.若年产量不足80台,则
万元.若年产量不足80台,则![]() ;若年产量不小于80台,则
;若年产量不小于80台,则![]() .每台设备售价为100万元,通过市场分析,该企业生产的设备能全部售完.
.每台设备售价为100万元,通过市场分析,该企业生产的设备能全部售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (台)的关系式;
(台)的关系式;
(2)年产量为多少台时,该企业所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知指数函数![]() 的图象经过点
的图象经过点![]() ,
,![]() 在区间
在区间![]() 的最小值
的最小值![]() ;
;
(1)求函数![]() 的解析式;
的解析式;
(2)求函数![]() 的最小值
的最小值![]() 的表达式;
的表达式;
(3)是否存在![]() 同时满足以下条件:①
同时满足以下条件:①![]() ;②当
;②当![]() 的定义域为
的定义域为![]() 时,值域为
时,值域为![]() ;若存在,求出m,n的值;若不存在,说明理由.
;若存在,求出m,n的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学有初中学生1800人,高中学生1200人.为了解全校学生本学期开学以来的课外阅读时间,学校采用分层抽样方法,从中抽取了100名学生进行问卷调查.将样本中的“初中学生”和“高中学生”,按学生的课外阅读时间(单位:小时)各分为5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得其频率分布直方图如图所示.
,得其频率分布直方图如图所示.
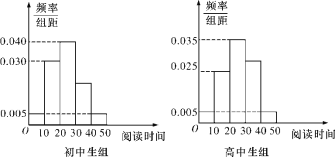
(1)估计全校学生中课外阅读时间在![]() 小时内的总人数约是多少;
小时内的总人数约是多少;
(2)从全校课外阅读时间不足10个小时的样本学生中随机抽取3人,求至少有2个初中生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,则直线
,则直线![]() 称为抛物线
称为抛物线![]() 的伴随直线.
的伴随直线.
(1)求抛物线![]() 的伴随直线的表达式;
的伴随直线的表达式;
(2)已知抛物线![]() 的伴随直线为
的伴随直线为![]() ,且该抛物线与
,且该抛物线与![]() 轴有两个不同的公共点,求
轴有两个不同的公共点,求![]() 的取值范围.
的取值范围.
(3)已知![]() ,若抛物线
,若抛物线![]() 的伴随直线为
的伴随直线为![]() ,且该抛物线与线段
,且该抛物线与线段![]() 恰有1个公共点,求
恰有1个公共点,求![]() 的取值范围(直接写出答案即可)
的取值范围(直接写出答案即可)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在以下命题中:
①三个非零向量![]() ,
,![]() ,
,![]() 不能构成空间的一个基底,则
不能构成空间的一个基底,则![]() ,
,![]() ,
,![]() 共面;
共面;
②若两个非零向量![]() ,
,![]() 与任何一个向量都不能构成空间的一个基底,则
与任何一个向量都不能构成空间的一个基底,则![]() ,
,![]() 共线;
共线;
③对空间任意一点![]() 和不共线的三点
和不共线的三点![]() ,
,![]() ,
,![]() ,若
,若![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() 四点共面
四点共面
④若![]() ,
,![]() 是两个不共线的向量,且
是两个不共线的向量,且![]() ,则
,则![]() 构成空间的一个基底
构成空间的一个基底
⑤若![]() 为空间的一个基底,则
为空间的一个基底,则![]() 构成空间的另一个基底;
构成空间的另一个基底;
其中真命题的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为双曲线
为双曲线![]() 的左、右焦点,过
的左、右焦点,过![]() 作垂直于
作垂直于![]() 轴的直线,并在
轴的直线,并在![]() 轴上方交双曲线于点
轴上方交双曲线于点![]() ,且
,且![]() .
.
(1)求双曲线![]() 的方程;
的方程;
(2)过双曲线![]() 上一点
上一点![]() 作两条渐近线的垂线,垂足分别是
作两条渐近线的垂线,垂足分别是![]() 和
和![]() ,试求
,试求![]() 的值;
的值;
(3)过圆![]() 上任意一点
上任意一点![]() 作切线
作切线![]() 交双曲线
交双曲线![]() 于
于![]() 两个不同点,
两个不同点,![]() 中点为
中点为![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高一年级6个班级去苏州、黄山、厦门三个地方修学旅行,每个城市至少有一个班前去,其中1班和2班不能去同一个地方,则共有_________种不同分配方法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地新建一家服装厂,从今年7月份开始投产,并且前4个月的产量分别为![]() 万件、
万件、![]() 万件、
万件、![]() 万件、
万件、![]() 万件.由于产品质量好,服装款式新颖,因此前几个月的产品销售情况良好.为了推销员在推销产品时接收订单不产生过多或过少的情况,需要估测以后几个月的产量,假如你是厂长,就月份x、产量y给出四种函数模型:
万件.由于产品质量好,服装款式新颖,因此前几个月的产品销售情况良好.为了推销员在推销产品时接收订单不产生过多或过少的情况,需要估测以后几个月的产量,假如你是厂长,就月份x、产量y给出四种函数模型:![]() ,
,![]() ,
,![]() ,
,![]() .你将利用零一种模型去估算以后几个月的产量?
.你将利用零一种模型去估算以后几个月的产量?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com