
【题目】已知等差数列![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)记数列![]() 的前
的前![]() 项和为
项和为![]() ,求
,求![]() ;
;
(3)是否存在正整数![]() ,使得
,使得![]() 仍为数列
仍为数列![]() 中的项,若存在,求出所有满足的正整数
中的项,若存在,求出所有满足的正整数![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
科目:高中数学 来源: 题型:
【题目】如图,已知矩形BB1C1C所在平面与底面ABB1N垂直,在直角梯形ABB1N中,AN∥BB1 , AB⊥AN,CB=BA=AN= ![]() BB1 .
BB1 . 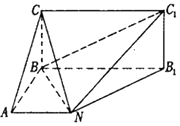
(1)求证:BN⊥平面C1B1N;
(2)求二面角C﹣C1N﹣B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ;
;
(1)若函数 ![]() 在
在 ![]() 上为增函数,求正实数
上为增函数,求正实数 ![]() 的取值范围;
的取值范围;
(2)当 ![]() 时,求函数
时,求函数 ![]() 在
在 ![]() 上的最值;
上的最值;
(3)当 ![]() 时,对大于1的任意正整数
时,对大于1的任意正整数 ![]() ,试比较
,试比较 ![]() 与
与 ![]() 的大小关系.
的大小关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种汽车购买时费用为16.9万元,每年应交付保险费、汽油费共0.9万元,汽车的维修保养费为:第一年0.2万元,第二年0.4万元,第三年0.6万元,……依等差数列逐年递增.
(1)求该车使用了3年的总费用(包括购车费用)为多少万元?
(2)设该车使用![]() 年的总费用(包括购车费用)为
年的总费用(包括购车费用)为![]() ),试写出
),试写出![]() 的表达式;
的表达式;
(3)求这种汽车使用多少年报废最合算(即该车使用多少年平均费用最少).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在考试测评中,常用难度曲线图来检测题目的质量,一般来说,全卷得分高的学生,在某道题目上的答对率也应较高,如果是某次数学测试压轴题的第1、2问得分难度曲线图,第1、2问满分均为6分,图中横坐标为分数段,纵坐标为该分数段的全体考生在第1、2问的平均难度,则下列说法正确的是( ) 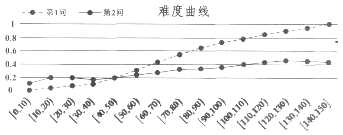
A.此题没有考生得12分
B.此题第1问比第2问更能区分学生数学成绩的好与坏
C.分数在[40,50)的考生此大题的平均得分大约为4.8分
D.全体考生第1问的得分标准差小于第2问的得分标准差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,![]() =2
=2![]() =2.
=2.
(1)求证:![]() ;
;
(2)求证:![]() ∥平面
∥平面![]() ;
;
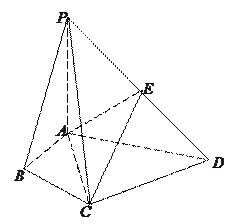
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的多面体ABCDEF中,四边形ABCD为正方形,底面ABFE为直角梯形,∠ABF为直角, ![]() , 平面ABCD⊥平面ABFE.
, 平面ABCD⊥平面ABFE.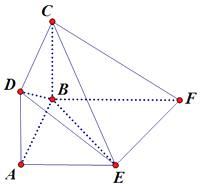
(1)求证:DB⊥EC;
(2)若AE=AB,求二面角C﹣EF﹣B的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com