
抛物线y=g(x)过点O(0,0)、A(m,0)与点P(m+1,m+1),其中m>n>0,b<a,设函数f(x)=(x﹣n)g(x)在x=a和x=b处取到极值.
(1)用m,x表示y=g(x)并比较a,b,m,n的大小(要求按从小到大排列);
(2)若![]() ,且过原点存在两条互相垂直的直线与曲线y=f(x)均相切,求y=f(x).
,且过原点存在两条互相垂直的直线与曲线y=f(x)均相切,求y=f(x).
考点:
直线与圆锥曲线的综合问题.
专题:
综合题.
分析:
(1)设抛物线方程,利用抛物线过点P,可得k=1,从而可得y=g(x)=x(x﹣m),利用函数f(x)在x=a和x=b处取到极值,结合m>n>0,即可比较a,b,m,n的大小;
(2)设切点Q(x0,y0),求导数,可得切线的方程,利用切线过原点,得两条两条切线的斜率,根据![]() ,两条切线垂直,即可求得函数解析式.
,两条切线垂直,即可求得函数解析式.
解答:
解:(1)由抛物线经过点O(0,0)、A(m,0)
设抛物线方程y=kx(x﹣m)(k≠0),
又抛物线过点P(m+1,m+1),则m+1=k(m+1)(m+1﹣m),得k=1,
所以y=g(x)=x(x﹣m). …(3分)
∴f(x)=(x﹣n)g(x)=x3﹣(m+n)x2+mnx,
∴f′(x)=3x2﹣2(m+n)x+mn,
∵函数f(x)在x=a和x=b处取到极值,…(5分)
∴f′(a)=0,f′(b)=0,
∵m>n>0,
∴f′(m)=3m2﹣2(m+n)m+mn=m(m﹣n)>0 …(7分)
f′(n)=3n2﹣2(m+n)n+mn=n(n﹣m)<0,
又b<a,故b<n<a<m. …(8分)
(2)设切点Q(x0,y0),则切线的斜率k=f′(x0)=3x02﹣2(m+n)x0+mn
又y0=![]() ﹣(m+n)
﹣(m+n)![]() +mnx0,所以切线的方程是y﹣
+mnx0,所以切线的方程是y﹣![]() +(m+n)
+(m+n)![]() ﹣mnx0=[3x02﹣2(m+n)x0+mn](x﹣x0)…(9分)
﹣mnx0=[3x02﹣2(m+n)x0+mn](x﹣x0)…(9分)
又切线过原点,故﹣![]() +(m+n)
+(m+n)![]() ﹣mnx0=[3x02﹣2(m+n)x0+mn](﹣x0)
﹣mnx0=[3x02﹣2(m+n)x0+mn](﹣x0)
所以2![]() ﹣(m+n)
﹣(m+n)![]() =0,解得x0=0,或x0=
=0,解得x0=0,或x0=![]() . …(10分)
. …(10分)
两条切线的斜率为k1=f′(0)=mn,![]() ,
,
由![]() ,得(m+n)2≥8,∴
,得(m+n)2≥8,∴![]() ,
,
∴![]() ,
,
所以![]() …(12分)
…(12分)
又两条切线垂直,故k1k2=﹣1,
所以上式等号成立,有![]() ,且mn=1.
,且mn=1.
所以f(x)=x3﹣(m+n)x2+mnx=x3﹣![]() x2+x. …13 分
x2+x. …13 分
点评:
本题考查导数知识的运用,考查导数的几何意义,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学河北省石家庄一中高三(上)第二次考试数学试卷(文科)(解析版) 题型:解答题
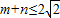 ,且过原点存在两条互相垂直的直线与曲线y=f(x)均相切,求y=f(x).
,且过原点存在两条互相垂直的直线与曲线y=f(x)均相切,求y=f(x).查看答案和解析>>
科目:高中数学 来源:2012-2013学河北省石家庄一中高三暑期第二次考试数学试卷(理科)(解析版) 题型:解答题
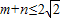 ,且过原点存在两条互相垂直的直线与曲线y=f(x)均相切,求y=f(x).
,且过原点存在两条互相垂直的直线与曲线y=f(x)均相切,求y=f(x).查看答案和解析>>
科目:高中数学 来源:2012-2013学河北省石家庄一中高三(上)第二次考试数学试卷(文科)(解析版) 题型:解答题
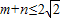 ,且过原点存在两条互相垂直的直线与曲线y=f(x)均相切,求y=f(x).
,且过原点存在两条互相垂直的直线与曲线y=f(x)均相切,求y=f(x).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com