Question

16．已知定义在R上的函数f（x）满足：①f（x）+f（2-x）=0；②f（x-2）=f（-x），③在[-1，1]上表达式为f（x）=$\sqrt{1-{x}^{2}}$，则函数f（x）与函数g（x）=$\left\{\begin{array}{l}{{2}^{x}，x≤0}\\{1-x，x＞0}\end{array}\right.$的图象在区间[-3，3]上的交点个数为（　　）

• A． 5
• B． 6
• C． 7
• D． 8

Answer 1

分析 由f（x）+f（2-x）=0，可得函数f（x）的图象关于点M（1，0）对称．由f（x-2）=f（-x），可得函数
f（x）的图象关于直线x=-1对称．画出f（x）在[-1，1]上的图象：进而得到在区间[-3，3]上的图象．画出函数g（x）在区间[-3，3]上的图象，即可得出交点个数．

解答 解：由f（x）+f（2-x）=0，可得函数f（x）的图象关于点M（1，0）对称．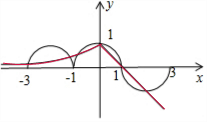
由f（x-2）=f（-x），可得函数f（x）的图象关于直线x=-1对称．
又在[-1，1]上表达式为f（x）=$\sqrt{1-{x}^{2}}$，可得图象：进而得到在区间[-3，3]上的图象．
画出函数g（x）=$\left\{\begin{array}{l}{{2}^{x}，x≤0}\\{1-x，x＞0}\end{array}\right.$在区间[-3，3]上的图象，
其交点个数为6个．
故选：B．

点评 本题考查了函数的图象与性质、数形结合思想方法，考查了推理能力与计算能力，属于中档题．