分析:(1)要证数列{a
n}是等比数列,只需利用已知条件证明
=是常数即可,利用通项公式的求法直接求其通项公式;
(2)要证
an≥1+,先验证n=1然后利用二项式定理,采用放缩法证明即可.
(3)若k=2,记
bn=| n |
 |
| i=0 |
(-1)i,求出b
n=2b
n-1-b
n-2,解得b
n=n+1,然后求b
2010.
解答:解:(1)对y=x
k求导数,得y
/=kx
k-1,切点是M
n(a
n,a
nk)的切线方程是y-a
nk=ka
nk-1(x-a
n).
当n=1时,切线过点P(1,0),即0-a
1k=ka
1k-1(x-a
1),得a
1=
,
当n>1时,切线过点P
n-1(a
n-1,0),即0-a
nk=ka
nk-1(a
n-1-a
n),得
=,
所以数列{a
n}是首项a
1=
,公比为
的等比数列,且通项公式为
an=()n.
(2)当n=1时,a
1=
=1+,当n≥2时,应用二项式定理,
an=()n=(1+)n=++()2++()n≥1+.
(3)a
n=2
n,b
n=
| n |
 |
| i=0 |
(-1)i22n-2i,设
cn=| n |
 |
| i=0 |
(-1)i22n-2i,
则b
n=2
2n+
| n |
 |
| i=1 |
(-1)i22n-2i(+)=| n |
 |
| i=0 |
(-1)i22n-2i-| n-1 |
 |
| j=0 |
(-1)j22(n-1)-2j=c
n-b
n-1.
同理c
n=2
2n+
| n-1 |
 |
| i=1 |
(-1)i22n-2i(+)+(-1)n=
| n-1 |
 |
| i=0 |
(-1)i22n-2i+
| n |
 |
| i=1 |
(-1)i22n-2i+| n |
 |
| i=1 |
(-1)i22n-2i=
4| n-1 |
 |
| i=0 |
(-1)i22(n-1)-2i-| n-1 |
 |
| k=0 |
(-1)k22(n-1)-2k=4b
n-1-C
n-1.
∴b
n+b
n-1=c
n=4b
n-1-c
n-1=4b
n-1-b
n-1-b
n-2,即b
n=2b
n-1-b
n-2,∴b
n-b
n-1=b
n-1-b
n-2═b
1-b
0=2-1=1,
故b
n=n+1,∴b
2010=2011.
点评:本题是中档题,考查数列的通项公式的求法,数列的证明,数列的化简与构造法的应用,是本题解题的关键,注意二项式定理的应用.
















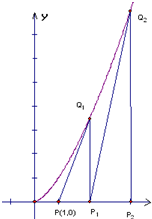 如图,过点P(1,0)作曲线C:y=xk(x∈(0,+∞),k∈N*,k>1)的切线,切点为Q1,设Q1点在x轴上的投影是点P1;又过点P1作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2;…;依此下去,得到一系列点Q1,Q2,…,Qn,…,设点Qn的横坐标为an.
如图,过点P(1,0)作曲线C:y=xk(x∈(0,+∞),k∈N*,k>1)的切线,切点为Q1,设Q1点在x轴上的投影是点P1;又过点P1作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2;…;依此下去,得到一系列点Q1,Q2,…,Qn,…,设点Qn的横坐标为an.

 (2009•锦州一模)过点P(1,0)作曲线C:y=x2(x>0)的切线,切点为Q1,没Q1在x轴上的投影是P1,又过P1,作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2…,依次下去,得到一系列点Q1Q2,…Qn,设Qn的横坐标为an.
(2009•锦州一模)过点P(1,0)作曲线C:y=x2(x>0)的切线,切点为Q1,没Q1在x轴上的投影是P1,又过P1,作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2…,依次下去,得到一系列点Q1Q2,…Qn,设Qn的横坐标为an.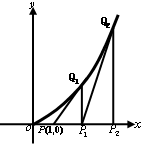 (2013•韶关二模)如图,过点P(1,0)作曲线C:y=x2(x∈(0,+∞))的切线,切点为Q1,设点Q1在x轴上的投影是点P1;又过点P1作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2;…;依此下去,得到一系列点Q1,Q2,Q3-Qn,设点Qn的横坐标为an.
(2013•韶关二模)如图,过点P(1,0)作曲线C:y=x2(x∈(0,+∞))的切线,切点为Q1,设点Q1在x轴上的投影是点P1;又过点P1作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2;…;依此下去,得到一系列点Q1,Q2,Q3-Qn,设点Qn的横坐标为an.