
【题目】已知数列![]() 中,
中,![]() ,
,![]() ,
,![]() ,且对
,且对![]() 时,有
时,有![]() .
.
(Ⅰ)设数列![]() 满足
满足![]() ,
,![]() ,证明数列
,证明数列![]() 为等比数列,并求数列
为等比数列,并求数列![]() 的通项公式;
的通项公式;
(Ⅱ)记![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】如图所示,沿河有A、B两城镇,它们相距![]() 千米.以前,两城镇的污水直接排入河里,现为保护环境,污水需经处理才能排放.两城镇可以单独建污水处理厂,或者联合建污水处理厂(在两城镇之间或其中一城镇建厂,用管道将污水从各城镇向污水处理厂输送).依据经验公式,建厂的费用为
千米.以前,两城镇的污水直接排入河里,现为保护环境,污水需经处理才能排放.两城镇可以单独建污水处理厂,或者联合建污水处理厂(在两城镇之间或其中一城镇建厂,用管道将污水从各城镇向污水处理厂输送).依据经验公式,建厂的费用为![]() (万元),
(万元),![]() 表示污水流量;铺设管道的费用(包括管道费)
表示污水流量;铺设管道的费用(包括管道费)![]() (万元),
(万元),![]() 表示输送污水管道的长度(千米).已知城镇A和城镇B的污水流量分别为
表示输送污水管道的长度(千米).已知城镇A和城镇B的污水流量分别为![]() 、
、![]() ,
,![]() 、
、![]() 两城镇连接污水处理厂的管道总长为
两城镇连接污水处理厂的管道总长为![]() 千米.假定:经管道输送的污水流量不发生改变,污水经处理后直接排入河中.请解答下列问题(结果精确到
千米.假定:经管道输送的污水流量不发生改变,污水经处理后直接排入河中.请解答下列问题(结果精确到![]() ):
):

(1)若在城镇A和城镇B单独建厂,共需多少总费用?
(2)考虑联合建厂可能节约总投资,设城镇A到拟建厂的距离为![]() 千米,求联合建厂的总费用
千米,求联合建厂的总费用![]() 与
与![]() 的函数关系式,并求
的函数关系式,并求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其导函数设为
,其导函数设为![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若函数![]() 有两个极值点
有两个极值点![]() ,
,![]() ,试用
,试用![]() 表示
表示![]() ;
;
(Ⅲ)在(Ⅱ)的条件下,若![]() 的极值点恰为
的极值点恰为![]() 的零点,试求
的零点,试求![]() ,
,![]() 这两个函数的所有极值之和的取值范围.
这两个函数的所有极值之和的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆心在曲线![]() 上,与直线x+y+1=0相切,且面积最小的圆的方程为( )
上,与直线x+y+1=0相切,且面积最小的圆的方程为( )
A. x2+(y-1)2=2B. x2+(y+1)2=2C. (x-1)2+y2=2D. (x+1)2+y2=2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
支付方式 | (0,1000] | (1000,2000] | 大于2000 |
仅使用A | 18人 | 9人 | 3人 |
仅使用B | 10人 | 14人 | 1人 |
(Ⅰ)从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率;
(Ⅱ)从样本仅使用A和仅使用B的学生中各随机抽取1人,以X表示这2人中上个月支付金额大于1000元的人数,求X的分布列和数学期望;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A的学生中,随机抽查3人,发现他们本月的支付金额都大于2000元.根据抽查结果,能否认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,有一个长方体形状的敞口玻璃容器,底面是边长为20cm的正方形,高为30cm,内有20cm深的溶液.现将此容器倾斜一定角度![]() (图②),且倾斜时底面的一条棱始终在桌面上(图①、②均为容器的纵截面).
(图②),且倾斜时底面的一条棱始终在桌面上(图①、②均为容器的纵截面).
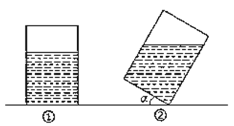
(1)要使倾斜后容器内的溶液不会溢出,角![]() 的最大值是多少?
的最大值是多少?
(2)现需要倒出不少于![]() 的溶液,当
的溶液,当![]() 时,能实现要求吗?请说明理由.
时,能实现要求吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com