
ЁОЬтФПЁПФГЙЋдАгаИіГиЬСЃЌЦфаЮзДЮЊжБНЧЁїABCЃЌ![]() ЃЌABЕФГЄЮЊ2АйУзЃЌBCЕФГЄЮЊ1АйУз.
ЃЌABЕФГЄЮЊ2АйУзЃЌBCЕФГЄЮЊ1АйУз.
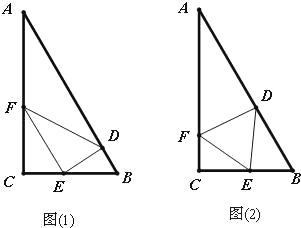
ЃЈ1ЃЉШєзМБИбјвЛХњЙЉгЮПЭЙлЩЭЕФгуЃЌЗжБ№дкABЁЂBCЁЂCAЩЯШЁЕуDЁЂEЁЂFЃЌШчЭМЃЈ1ЃЉЃЌЪЙЕУ![]() ЃЌ
ЃЌ![]() ЃЌдкЁїDEFФкЮЙЪГЃЌЧѓЕБЁїDEFЕФУцЛ§ШЁзюДѓжЕЪБEFЕФГЄЃЛ
ЃЌдкЁїDEFФкЮЙЪГЃЌЧѓЕБЁїDEFЕФУцЛ§ШЁзюДѓжЕЪБEFЕФГЄЃЛ
ЃЈ2ЃЉШєзМБИНЈдьвЛИіКЩЬСЃЌЗжБ№дкABЁЂBCЁЂCAЩЯШЁЕуDЁЂEЁЂFЃЌШчЭМЃЈ2ЃЉЃЌНЈдьЁїDEFСЌРШЃЈВЛПМТЧПэЖШЃЉЙЉгЮПЭанэЌЃЌЧвЪЙЁїDEFЮЊе§Ш§НЧаЮЃЌМЧ![]() ЃЌЧѓЁїDEFБпГЄЕФзюаЁжЕМАДЫЪБ
ЃЌЧѓЁїDEFБпГЄЕФзюаЁжЕМАДЫЪБ![]() ЕФжЕ.ЃЈОЋШЗЕН1УзКЭ0.1ЖШЃЉ
ЕФжЕ.ЃЈОЋШЗЕН1УзКЭ0.1ЖШЃЉ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉзюаЁжЕЪЧ65УзЃЌ
ЃЛЃЈ2ЃЉзюаЁжЕЪЧ65УзЃЌ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЩшEFЃНxЃЌдђПЩЧѓCEЃЌBEЃЌDEЃЌЧѓЕУSЁїDEF![]() xЃЈ1
xЃЈ1![]() ЃЉЃЌxЁЪЃЈ0ЃЌ2ЃЉЃЌгЩЛљБОВЛЕШЪНПЩЕУЃК
ЃЉЃЌxЁЪЃЈ0ЃЌ2ЃЉЃЌгЩЛљБОВЛЕШЪНПЩЕУЃК![]() ЃЈ1
ЃЈ1![]() ЃЉ
ЃЉ![]() ЃЈ
ЃЈ![]() ЃЉ2ЕБЧвНіЕБxЃН1ЪБЕШКХГЩСЂЃЌДгЖјПЩЧѓЕБЁїDEFЕФУцЛ§ШЁзюДѓжЕЪБEFЕФГЄЃЛ
ЃЉ2ЕБЧвНіЕБxЃН1ЪБЕШКХГЩСЂЃЌДгЖјПЩЧѓЕБЁїDEFЕФУцЛ§ШЁзюДѓжЕЪБEFЕФГЄЃЛ
ЃЈ2ЃЉЩшЕШБпШ§НЧаЮБпГЄЮЊEFЃНEDЃНDFЃНyЃЌдкЁїEBDжаЃЌгЩе§ЯвЖЈРэМАШ§НЧКЏЪ§ЕФаджЪПЩЕУy![]() 0.65ЃЌМДПЩЧѓЕУЁїDEFБпГЄЕФзюаЁжЕМАДЫЪБІСЕФжЕЃЎ
0.65ЃЌМДПЩЧѓЕУЁїDEFБпГЄЕФзюаЁжЕМАДЫЪБІСЕФжЕЃЎ
ЃЈ1ЃЉЩш![]() ЃЌдђ
ЃЌдђ![]() ЃЌЙЪ
ЃЌЙЪ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌSЁїDEF
ЃЌSЁїDEF![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
вђЮЊSЁїDEF![]() ЕБЧвНіЕБ
ЕБЧвНіЕБ![]() ЃЈМДEFГЄ100УзЃЉЪБЕШКХГЩСЂЃЌ
ЃЈМДEFГЄ100УзЃЉЪБЕШКХГЩСЂЃЌ
МДЃЈSЁїDEЃЉmax![]() .
.
ЃЈ2ЃЉЩшЕШБпШ§НЧаЮБпГЄЮЊ![]() ЃЌдкЁїEBDжаЃЌ
ЃЌдкЁїEBDжаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
гЩЬтвтПЩжЊ![]() ЃЌдђ
ЃЌдђ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌ
ЃЌ
МД![]() ЃЌМДЁїDEFБпГЄЕФзюаЁжЕЪЧ65УзЃЌ
ЃЌМДЁїDEFБпГЄЕФзюаЁжЕЪЧ65УзЃЌ
ДЫЪБ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЧЮоЧюЪ§Са![]() ЕФЧА
ЕФЧА![]() ЯюжазюДѓжЕЮЊ
ЯюжазюДѓжЕЮЊ![]() ЃЌзюаЁжЕЮЊ
ЃЌзюаЁжЕЮЊ![]() ЃЌСю
ЃЌСю![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШє![]() ЃЌаДГі
ЃЌаДГі![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЩш![]() ЃЌШє
ЃЌШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕМА
ЕФжЕМА![]() ЪБЪ§Са
ЪБЪ§Са![]() ЕФЧА
ЕФЧА![]() ЯюКЭ
ЯюКЭ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЧѓжЄЃКЁАЪ§Са![]() ЪЧЕШВюЪ§СаЁБЕФГфвЊЬѕМўЪЧЁАЪ§Са
ЪЧЕШВюЪ§СаЁБЕФГфвЊЬѕМўЪЧЁАЪ§Са![]() ЪЧЕШВюЪ§СаЁБЃЎ
ЪЧЕШВюЪ§СаЁБЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЦпЧЩАхЪЧЙХДњжаЙњРЭЖЏШЫУёЗЂУїЕФвЛжжжаЙњДЋЭГжЧСІЭцОпЃЌЫќгЩЮхПщЕШбќжБНЧШ§НЧаЮЃЌвЛПще§ЗНаЮКЭвЛПщЦНааЫФБпаЮЙВЦпПщАхзщГЩ.ЧхТНвдЁЖРфТЎдгЪЖЁЗОэвЛжааДЕРЃКНќгжгаЦпЧЩЭМЃЌЦфЪНЮхЃЌЦфЪ§ЦпЃЌЦфБфЛЏжЎЪНЖржСЧЇгр.ЬхЮяаЄаЮЃЌЫцЪжБфЛУЃЌИЧгЮЯЗжЎОпЃЌзувдХХУЦЦЦМХЃЌЙЪЪРЫзНдЯВЮЊжЎ.ШчЭМЪЧвЛИігУЦпЧЩАхЦДГЩЕФе§ЗНаЮЃЌШєдкДЫе§ЗНаЮжаШЮШЁвЛЕуЃЌдђДЫЕуШЁздвѕгАВПЗжЕФИХТЪЮЊЃЈ ЃЉ

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП[бЁао4Ѓ4ЃКзјБъЯЕгыВЮЪ§ЗНГЬ]
дкЦНУцжБНЧзјБъЯЕ![]() жа,вд
жа,вд![]() ЮЊМЋЕуЃЌ
ЮЊМЋЕуЃЌ![]() жсЕФе§АыжсЮЊМЋжсЃЌНЈСЂМЋзјБъЯЕЃЌЧњЯп
жсЕФе§АыжсЮЊМЋжсЃЌНЈСЂМЋзјБъЯЕЃЌЧњЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() ЃЛжБЯп
ЃЛжБЯп![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ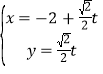 (tЮЊВЮЪ§ЃЉ.жБЯп
(tЮЊВЮЪ§ЃЉ.жБЯп![]() гыЧњЯп
гыЧњЯп![]() ЗжБ№НЛгк
ЗжБ№НЛгк![]() СНЕу.
СНЕу.
ЃЈ1ЃЉаДГіЧњЯп![]() ЕФжБНЧзјБъЗНГЬКЭжБЯп
ЕФжБНЧзјБъЗНГЬКЭжБЯп![]() ЕФЦеЭЈЗНГЬЃЛ
ЕФЦеЭЈЗНГЬЃЛ
ЃЈ2ЃЉШєЕу![]() ЕФМЋзјБъЮЊ
ЕФМЋзјБъЮЊ![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙ§ХзЮяЯпy2ЃН8xЕФНЙЕуЃЌзїЧуаБНЧЮЊ45ЁуЕФжБЯпЃЌдђБЛХзЮяЯпНиЕУЕФЯвГЄЮЊ(ЁЁЁЁ)
A. 8 B. 16 C. 32 D. 64
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєЮоЧюЪ§Са![]() ТњзуЃКжЛвЊ
ТњзуЃКжЛвЊ![]() ЃЌБига
ЃЌБига![]() ЃЌдђГЦ
ЃЌдђГЦ![]() ОпгааджЪ
ОпгааджЪ![]() .
.
ЃЈ1ЃЉШє![]() ОпгааджЪ
ОпгааджЪ![]() ЃЌЧв
ЃЌЧв![]() ЃЌ
ЃЌ ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШєЮоЧюЪ§Са![]() ЪЧЕШВюЪ§СаЃЌЮоЧюЪ§Са
ЪЧЕШВюЪ§СаЃЌЮоЧюЪ§Са![]() ЪЧЙЋБШЮЊе§Ъ§ЕФЕШБШЪ§СаЃЌ
ЪЧЙЋБШЮЊе§Ъ§ЕФЕШБШЪ§СаЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ХаЖЯ
ХаЖЯ![]() ЪЧЗёОпгааджЪ
ЪЧЗёОпгааджЪ![]() ЃЌВЂЫЕУїРэгЩЃЛ
ЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЩш![]() ЪЧЮоЧюЪ§СаЃЌвбжЊ
ЪЧЮоЧюЪ§СаЃЌвбжЊ![]() .ЧѓжЄЃКЁАЖдШЮвт
.ЧѓжЄЃКЁАЖдШЮвт![]() ЖМОпгааджЪ
ЖМОпгааджЪ![]() ЁБЕФГфвЊЬѕМўЮЊЁА
ЁБЕФГфвЊЬѕМўЮЊЁА![]() ЪЧГЃЪ§СаЁБ.
ЪЧГЃЪ§СаЁБ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮ![]() ЮЊе§ЗНаЮЃЌ
ЮЊе§ЗНаЮЃЌ![]() ЃЌЧв
ЃЌЧв![]() ЃЌ
ЃЌ![]() ЦНУц
ЦНУц![]() .
.
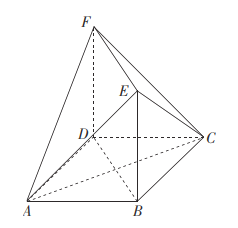
ЃЈ1ЃЉжЄУїЃКЦНУц![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓЖўУцНЧ![]() ЕФгрЯвжЕ.
ЕФгрЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдкОиаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЁЂ
ЁЂ![]() ЗжБ№дкЯпЖЮ
ЗжБ№дкЯпЖЮ![]() ЁЂ
ЁЂ![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() ЃЌ
ЃЌ![]() ЃЌЯжНЋ
ЃЌЯжНЋ![]() би
би![]() елЕН
елЕН![]() ЕФЮЛжУЃЌСЌНс
ЕФЮЛжУЃЌСЌНс![]() ЃЌ
ЃЌ![]() ЃЌШчЭМ2
ЃЌШчЭМ2
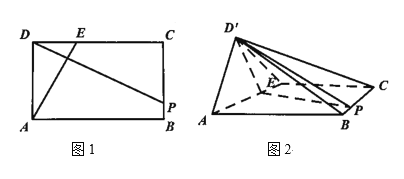
ЃЈ1ЃЉжЄУїЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉМЧЦНУц![]() гыЦНУц
гыЦНУц![]() ЕФНЛЯпЮЊ
ЕФНЛЯпЮЊ![]() .ШєЖўУцНЧ
.ШєЖўУцНЧ![]() ЮЊ
ЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() гыЦНУц
гыЦНУц![]() ЫљГЩНЧЕФе§ЯвжЕ.
ЫљГЩНЧЕФе§ЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ЕФзѓЖЅЕуЮЊ
ЕФзѓЖЅЕуЮЊ![]() ЃЌСНИіНЙЕугыЖЬжсвЛИіЖЅЕуЙЙГЩЕШбќжБНЧШ§НЧаЮЃЌЙ§Еу
ЃЌСНИіНЙЕугыЖЬжсвЛИіЖЅЕуЙЙГЩЕШбќжБНЧШ§НЧаЮЃЌЙ§Еу![]() ЧвгыxжсВЛжиКЯЕФжБЯпlгыЭждВНЛгкMЃЌNВЛЭЌЕФСНЕуЃЎ
ЧвгыxжсВЛжиКЯЕФжБЯпlгыЭждВНЛгкMЃЌNВЛЭЌЕФСНЕуЃЎ
ЃЈЂёЃЉЧѓЭждВPЕФЗНГЬЃЛ
ЃЈЂђЃЉЕБAMгыMNДЙжБЪБЃЌЧѓAMЕФГЄЃЛ
ЃЈЂѓЃЉШєЙ§ЕуPЧвЦНаагкAMЕФжБЯпНЛжБЯп![]() гкЕуQЃЌЧѓжЄЃКжБЯпNQКуЙ§ЖЈЕуЃЎ
гкЕуQЃЌЧѓжЄЃКжБЯпNQКуЙ§ЖЈЕуЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com