
某公司为了实现1000万元利润的目标,准备制定一个激励销售部门的奖励方案;在销售利润达到10万元时,按销售利润进行奖励,且奖金![]() (单位:万元)随销售利润
(单位:万元)随销售利润![]() (单位:万元)的增加而增加,但奖金总数不超过
(单位:万元)的增加而增加,但奖金总数不超过![]() 万元,同时奖金不超过利润的
万元,同时奖金不超过利润的![]() .现有三个奖励模型:
.现有三个奖励模型:![]() ,
,![]() ,
,![]() .其中哪个模型能符合公司的要求?
.其中哪个模型能符合公司的要求?
模型![]() 确实能符合公司要求
确实能符合公司要求
借助计算器或计算机作出函数![]() ,
,![]() ,
,![]() ,
,
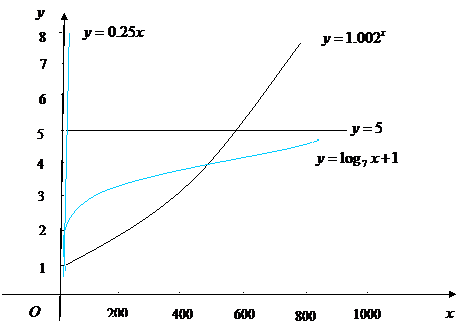
![]() 的图象,观察图象发现,在区间
的图象,观察图象发现,在区间![]() 上,模型
上,模型![]() ,
,![]() 的图象都有一部分在直线
的图象都有一部分在直线![]() 的上方,只有模型
的上方,只有模型![]() 的图象始终在
的图象始终在![]() 的下方,这说明只有按模型
的下方,这说明只有按模型![]() 进行奖励时才符合公司的要求.下面通过计算确认上述判断.
进行奖励时才符合公司的要求.下面通过计算确认上述判断.
 |
首先计算哪个模型的奖金总数不超过![]() 万.
万.
对于模型![]() ,它在区间
,它在区间![]() 上递增,当
上递增,当![]() 时,
时,![]() ,因此该模型不符合要求;
,因此该模型不符合要求;
对于模型![]() ,由函数图象,并利用计算器,可知在区间
,由函数图象,并利用计算器,可知在区间![]() 内有一个点
内有一个点![]() 满足
满足![]() ,由于它在区间
,由于它在区间![]() 上递增,因此当
上递增,因此当![]() 时,
时,![]() ,因此该模型也不符合要求;
,因此该模型也不符合要求;
对于模型![]() ,它在区间
,它在区间![]() 上递增,而且当
上递增,而且当![]() 时,
时,![]() ,所以它符合奖金总数不超过
,所以它符合奖金总数不超过![]() 万元的要求.
万元的要求.
再计算按模型![]() 奖励时,奖金是否不超过利润的
奖励时,奖金是否不超过利润的![]() ,
,
即当![]() 时,是否有
时,是否有![]() 成立.
成立.
令![]() ,
,![]() .
.
利用计算器或计算机作出函数![]() 的图象,
的图象,
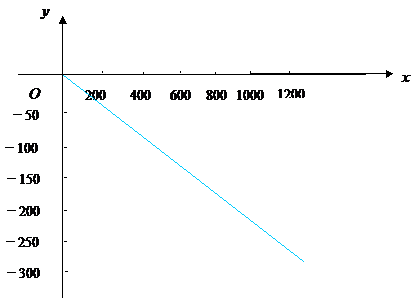 |
由图象可知它是递减的,因此![]() ,即
,即![]() .
.
所以,当![]() 时,
时,![]() .说明按模型
.说明按模型![]() 奖励,奖金不会超过利润的
奖励,奖金不会超过利润的![]() .
.
综上所述,模型![]() 确实能符合公司要求.
确实能符合公司要求.


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省高三第二次质量检测理科数学试卷(解析版) 题型:解答题
某公司为了实现1000万元利润的目标,准备制定一个激励销售人员的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金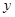 (单位:万元)随销售利润
(单位:万元)随销售利润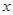 (单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不能超过利润的
(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不能超过利润的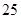 %.现有三个奖励模型:
%.现有三个奖励模型: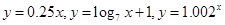 ,分析与推导哪个函数模型能符合该公司的要求?并给予证明.(注:
,分析与推导哪个函数模型能符合该公司的要求?并给予证明.(注: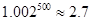 )
)
查看答案和解析>>
科目:高中数学 来源:2013年四川省泸州市高考数学一模试卷(理科)(解析版) 题型:选择题
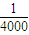 x2
x2查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com