
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的右焦点为F(1,0),且点P(1,
=1(a>b>0)的右焦点为F(1,0),且点P(1, ![]() )在椭圆C上,O为坐标原点.
)在椭圆C上,O为坐标原点.
(1)求椭圆C的标准方程;
(2)设过定点T(0,2)的直线l与椭圆C交于不同的两点A、B,且∠AOB为锐角,求直线l的斜率k的取值范围;
(3)过椭圆C1: ![]() +
+ ![]() =1上异于其顶点的任一点P,作圆O:x2+y2=
=1上异于其顶点的任一点P,作圆O:x2+y2= ![]() 的两条切线,切点分别为M,N(M,N不在坐标轴上),若直线MN在x轴、y轴上的截距分别为m、n,证明:
的两条切线,切点分别为M,N(M,N不在坐标轴上),若直线MN在x轴、y轴上的截距分别为m、n,证明: ![]() +
+ ![]() 为定值.
为定值.
【答案】
(1)解:由题意得:c=1,
∴a2=b2+1,
又因为点P(1, ![]() )在椭圆C上,
)在椭圆C上,
∴ ![]() +
+ ![]() =1,
=1,
解得:a2=4,b2=3,
则椭圆标准方程为 ![]() +
+ ![]() =1
=1
(2)解:设直线l方程为y=kx+2,A(x1,y1)、B(x2,y2),
联立  ,消去y得:(4k2+3)x2+16kx+4=0,
,消去y得:(4k2+3)x2+16kx+4=0,
∵△=12k2﹣3>0,∴k2> ![]() ,
,
∴x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,
,
∵∠AOB为锐角,∴ ![]()
![]() >0,即x1x2+y1y2>0,
>0,即x1x2+y1y2>0,
∴x1x2+(kx1+2)(kx2+2)>0,即(1+k2)x1x2+2k(x1+x2)+4>0,
整理得:(1+k2) ![]() +2k
+2k ![]() +4>0,即
+4>0,即 ![]() >0,
>0,
整理得:k2< ![]() ,即
,即 ![]() <k2<
<k2< ![]() ,
,
解得:﹣ ![]() <k<﹣
<k<﹣ ![]() 或
或 ![]() <k<
<k< ![]()
(3)解:由题意:C1: ![]() +
+ ![]() =1,
=1,
设点P(x1,y1),M(x2,y2),N(x3,y3),
∵M,N不在坐标轴上,∴kPM=﹣ ![]() =﹣
=﹣ ![]() ,
,
∴直线PM的方程为y﹣y2=﹣ ![]() (x﹣x2),
(x﹣x2),
化简得:x2x+y2y= ![]() ④,
④,
同理可得直线PN的方程为x3x+y3y= ![]() ⑤,
⑤,
把P点的坐标代入④、⑤得  ,
,
∴直线MN的方程为x1x+y1y= ![]() ,
,
令y=0,得m= ![]() ,令x=0得n=
,令x=0得n= ![]() ,
,
∴x1= ![]() ,y1=
,y1= ![]() ,
,
又点P在椭圆C1上,
∴( ![]() )2+3(
)2+3( ![]() )2=4,
)2=4,
则 ![]() +
+ ![]() =
= ![]() 为定值
为定值
【解析】(1)由焦点坐标确定出c的值,根据椭圆的性质列出a与b的方程,再将P点坐标代入椭圆方程列出关于a与b的方程,联立求出a与b的值,确定出椭圆方程即可;(2)设直线l方程为y=kx+2,A(x1 , y1)、B(x2 , y2),联立l与椭圆方程,消去y得到关于x的一元二次方程,利用韦达定理表示出x1+x2与x1x2 , 根据∠AOB为锐角,得到 ![]()
![]() >0,即x1x2+y1y2>0,即可确定出k的范围;(3)由题意:确定出C1的方程,设点P(x1 , y1),M(x2 , y2),N(x3 , y3),根据M,N不在坐标轴上,得到直线PM与直线OM斜率乘积为﹣1,确定出直线PM的方程,同理可得直线PN的方程,进而确定出直线MN方程,求出直线MN与x轴,y轴截距m与n,即可确定出所求式子的值为定值.
>0,即x1x2+y1y2>0,即可确定出k的范围;(3)由题意:确定出C1的方程,设点P(x1 , y1),M(x2 , y2),N(x3 , y3),根据M,N不在坐标轴上,得到直线PM与直线OM斜率乘积为﹣1,确定出直线PM的方程,同理可得直线PN的方程,进而确定出直线MN方程,求出直线MN与x轴,y轴截距m与n,即可确定出所求式子的值为定值.
【考点精析】本题主要考查了椭圆的标准方程的相关知识点,需要掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能正确解答此题.
才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
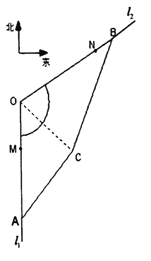
【题目】已知![]() 分别是海岸线
分别是海岸线![]() 上的三个集镇,
上的三个集镇, ![]() 位于
位于![]() 的正南方向
的正南方向![]() 处,
处, ![]() 位于
位于![]() 的北偏东60°方向
的北偏东60°方向![]() 处;
处;
(1)为了缓解集镇![]() 的交通压力,拟在海岸线
的交通压力,拟在海岸线![]() 上分别修建码头
上分别修建码头![]() ,开辟水上直达航线,使
,开辟水上直达航线,使![]() ,
, ![]() .勘测时发现以
.勘测时发现以![]() 为圆心,
为圆心, ![]() 为半径的扇形区域为浅水区,不适宜船只航行,问此航线是否影响船只航行?
为半径的扇形区域为浅水区,不适宜船只航行,问此航线是否影响船只航行?
(2)为了发展经济需要,政府计划填海造陆,建造一个商业区(如图四边形![]() 所示),其中
所示),其中![]() ,
, ![]() ,
, ![]() ,求该商业区的面积
,求该商业区的面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海关对同时从![]() 三个不同地区进口的某种商品进行随机抽样检测,已知从
三个不同地区进口的某种商品进行随机抽样检测,已知从![]() 三个地区抽取的商品件数分别是50,150,100.检测人员再用分层抽样的方法从海关抽样的这些商品中随机抽取6件样品进行检测.
三个地区抽取的商品件数分别是50,150,100.检测人员再用分层抽样的方法从海关抽样的这些商品中随机抽取6件样品进行检测.
(1)求这6件样品中,来自![]() 各地区商品的数量;
各地区商品的数量;
(2)若在这6件样品中随机抽取2件送往另一机构进行进一步检测,求这2件样品来自相同地区的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种新产品投放市场的100天中,前40天价格呈直线上升,而后60天其价格呈直线下降,现统计出其中4天的价格如下表:
时间 | 第4天 | 第32天 | 第60天 | 第90天 |
价格(千元) | 23 | 30 | 22 | 7 |
(1)写出价格![]() 关于时间
关于时间![]() 的函数关系式;(
的函数关系式;(![]() 表示投放市场的第
表示投放市场的第![]() 天);
天);
(2)销售量![]() 与时间
与时间![]() 的函数关系:
的函数关系:![]() ,则该产品投放市场第几天销售额最高?最高为多少千元?
,则该产品投放市场第几天销售额最高?最高为多少千元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从一堆产品![]() 正品与次品都多于2件
正品与次品都多于2件![]() 中任取2件,观察正品件数和次品件数,则下列说法:
中任取2件,观察正品件数和次品件数,则下列说法:
![]() “恰好有1件次品”和“恰好2件都是次品”是互斥事件
“恰好有1件次品”和“恰好2件都是次品”是互斥事件
![]() “至少有1件正品”和“全是次品”是对立事件
“至少有1件正品”和“全是次品”是对立事件
![]() “至少有1件正品”和“至少有1件次品”是互斥事件但不是对立事件
“至少有1件正品”和“至少有1件次品”是互斥事件但不是对立事件
![]() “至少有1件次品”和“全是正品”是互斥事件也是对立事件
“至少有1件次品”和“全是正品”是互斥事件也是对立事件
其中正确的有______![]() 填序号
填序号![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题![]() 方程
方程![]() 表示焦点在
表示焦点在![]() 轴上的椭圆;命题
轴上的椭圆;命题![]() 方程
方程![]() 表示的曲线是双曲线.
表示的曲线是双曲线.
(1)若“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围;
的取值范围;
(2)若“![]() ”为假命题、且“
”为假命题、且“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com