已知函数f(x)=x3+ax2+bx+a2在x=1处有极值10,求实数a,b的值;并判断f(1)=10是极大值还是极小值.
解:∵函数f(x)=x
3+ax
2+bx+a
2∴f'(x)=3x
2+2ax+b,
又∵函数f(x)=x
3+ax
2+bx+a
2在x=1处有极值10,
∴
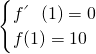
解得:

或
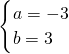
当a=4,b=-11时,
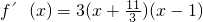
,f(x)在

,在
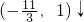
,在(1,+∞)↑
∴f(x)在x=1处取得极小值f(1)=10;
当a=-3,b=3时,f'(x)=3(x-1)
2≥0,f(x)在R上单增,无极值.
∴a=4,b=-11;且f(1)=10是极小值.
分析:根据已知中函数f(x)=x
3+ax
2+bx+a
2在x=1处有极值10,我们可得到
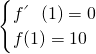
,根据函数f(x)=x
3+ax
2+bx+a
2,求出导函数的解析式后,构造关于a,b的方程,解方程即可求出a,b的,根据第一步中a,b的值,我们求出函数的解析式,分析函数在X=1两侧的单调性,即可判断出f(1)=10是极大值还是极小值.
点评:本题考查的知识点是函数在某点取得极值的条件,利用导数研究函数的极值,其中根据已知条件,构造关于a,b的方程,是解答本题的关键,在解答过程中,解方程组
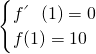
,可以求出两组满足条件的a,b的值,其中一组可导致f(x)在R上单增,不满足题目要求,要舍去,这是本题解答中的一个易忽略点.

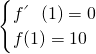 解得:
解得: 或
或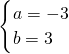
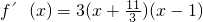 ,f(x)在
,f(x)在 ,在
,在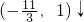 ,在(1,+∞)↑
,在(1,+∞)↑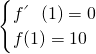 ,根据函数f(x)=x3+ax2+bx+a2,求出导函数的解析式后,构造关于a,b的方程,解方程即可求出a,b的,根据第一步中a,b的值,我们求出函数的解析式,分析函数在X=1两侧的单调性,即可判断出f(1)=10是极大值还是极小值.
,根据函数f(x)=x3+ax2+bx+a2,求出导函数的解析式后,构造关于a,b的方程,解方程即可求出a,b的,根据第一步中a,b的值,我们求出函数的解析式,分析函数在X=1两侧的单调性,即可判断出f(1)=10是极大值还是极小值.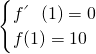 ,可以求出两组满足条件的a,b的值,其中一组可导致f(x)在R上单增,不满足题目要求,要舍去,这是本题解答中的一个易忽略点.
,可以求出两组满足条件的a,b的值,其中一组可导致f(x)在R上单增,不满足题目要求,要舍去,这是本题解答中的一个易忽略点. 

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<