
| A. | [1,+∞) | B. | $[{1,\frac{1}{2}+ln2}]$ | C. | (-∞,e-1] | D. | [1,e-1] |
分析 由clnb=a+clnc化为lnb=$\frac{a}{c}$+lnc,可得ln$\frac{b}{a}$=lnlnb-lna=$\frac{a}{c}$+lnc-lna=$\frac{a}{c}$+ln $\frac{c}{a}$,令 $\frac{c}{a}$=x,可得ln $\frac{b}{a}$=f(x)=$\frac{1}{x}$+lnx,$\frac{1}{e}$≤x≤2.再利用导数研究其单调性极值与最值即可.
解答 解:由clnb=a+clnc化为lnb=$\frac{a}{c}$+lnc,
∴ln$\frac{b}{a}$=lnb-lna=$\frac{a}{c}$+lnc-lna=$\frac{a}{c}$+ln$\frac{c}{a}$,
令$\frac{c}{a}$=x,则ln$\frac{b}{a}$=f(x)=$\frac{1}{x}$+lnx,$\frac{1}{e}$≤x≤2.
f′(x)=-$\frac{1}{{x}^{2}}$+$\frac{1}{x}$=$\frac{x-1}{{x}^{2}}$,令f′(x)=0,解得x=1.
当$\frac{1}{e}$≤x<1时,f′(x)<0,函数f(x)单调递减;
当1<x≤2时,f′(x)>0,函数f(x)单调递增.
∴当x=1时,函数f(x)取得极小值即最小值,f(1)=1+ln1=1.
又f(2)=$\frac{1}{2}$+ln2,f($\frac{1}{e}$)=e+ln$\frac{1}{e}$=e-1,
f($\frac{1}{e}$)-f(2)=e-ln2-$\frac{3}{2}$>e-lne-$\frac{3}{2}$=e-2.5>0,
∴e-1>$\frac{1}{2}$+ln2,
因此f(x)的最大值为e-1.
综上可得:f(x)∈[1,e-1].
即ln$\frac{b}{a}$的取值范围是[1,e-1].
故选:D.
点评 本题考查了经过变形把问题转化为利用导数研究其单调性极值与最值,考查了推理能力和解决问题的能力,属于难题.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
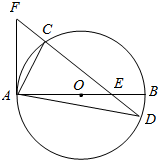 如图AB是圆O的直径,AF⊥AB,弦CD交AB、AF分别于E、F,交圆于点C.
如图AB是圆O的直径,AF⊥AB,弦CD交AB、AF分别于E、F,交圆于点C.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
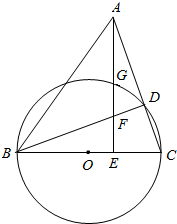 如图,以△ABC的边BC为直径作圆O交AC于D,过A点作AE⊥BC于E,AE交圆O于点G,交BD于点F.
如图,以△ABC的边BC为直径作圆O交AC于D,过A点作AE⊥BC于E,AE交圆O于点G,交BD于点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
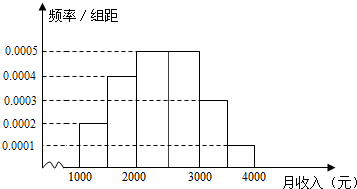 某市统计局就某地居民的月收入调查了10 000人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1 000,1 500)内).根据频率分布直方图算出样本数据的中位数是( )
某市统计局就某地居民的月收入调查了10 000人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1 000,1 500)内).根据频率分布直方图算出样本数据的中位数是( )| A. | 2360 | B. | 2380 | C. | 2400 | D. | 2420 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com