
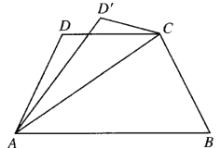
【题目】如图,已知四边形![]() 是底角为
是底角为![]() 的等腰梯形,且
的等腰梯形,且![]() ,沿直线
,沿直线![]() 将
将![]() 翻折成
翻折成![]() ,所成二面角
,所成二面角![]() 的平面角为
的平面角为![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:高中数学 来源: 题型:
【题目】已知正方体![]() 的棱长为
的棱长为![]() 为
为![]() 的中点,下列说法中正确的是( )
的中点,下列说法中正确的是( )
A.![]() 与
与![]() 所成的角大于
所成的角大于![]()
B.点![]() 到平面
到平面![]() 的距离为1
的距离为1
C.三棱锥![]() 的外接球的表面积为
的外接球的表面积为![]()
D.直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】个人所得税是国家对本国公民、居住在本国境内的个人的所得和境外个人来源于本国的所得征收的一种所得税.我国在1980年9月10日,第五届全国人民代表大会第三次会议通过并公布了《中华人民共和国个人所得税法》.公民依法诚信纳税是义务,更是责任现将自2013年至2017年的个人所得税收入统计如下

并制作了时间代号x与个人所得税收入的如如图所示的散点图:
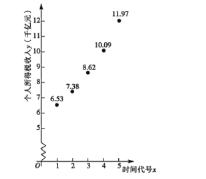
根据散点图判断,可用①y=menx与②![]() 作为年个人所得税收入y关于时间代号x的回归方程,经过数据运算和处理,得到如下数据:
作为年个人所得税收入y关于时间代号x的回归方程,经过数据运算和处理,得到如下数据:

以下计算过程中四舍五入保留两位小数.
(1)根据所给数据,分别求出①,②中y关于x的回归方程;
(2)已知2018年个人所得税收人为13.87千亿元,用2018年的数据验证(1)中所得两个回归方程,哪个更适宜作为y关于时间代号x的回归方程?
(3)你还能从统计学哪些角度来进一步确认哪个回归方程更适宜? (只需叙述,不必计算)
附:对于一组数据![]() 其回归直线
其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: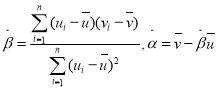
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B是抛物线![]() 上的两点,且在x轴两侧,若AB的中点为Q,分别过A,B两点作T的切线,且两切线相交于点P.
上的两点,且在x轴两侧,若AB的中点为Q,分别过A,B两点作T的切线,且两切线相交于点P.
(1)求证:直线PQ平行于x轴;
(2)若直线AB经过抛物线T的焦点,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年春季,某出租汽车公司决定更换一批新的小汽车以代替原来报废的出租车,现有采购成本分别为![]() 万元/辆和
万元/辆和![]() 万元/辆的
万元/辆的![]() 两款车型,根据以往这两种出租车车型的数据,得到两款出租车车型使用寿命频数表如下:
两款车型,根据以往这两种出租车车型的数据,得到两款出租车车型使用寿命频数表如下:
使用寿命年数 | 5年 | 6年 | 7年 | 8年 | 总计 |
| 10 | 20 | 45 | 25 | 100 |
| 15 | 35 | 40 | 10 | 100 |
(1)填写下表,并判断是否有![]() 的把握认为出租车的使用寿命年数与汽车车型有关?
的把握认为出租车的使用寿命年数与汽车车型有关?
使用寿命不高于 | 使用寿命不低于 | 总计 | |
| |||
| |||
总计 |
(2)从![]() 和
和![]() 的车型中各随机抽取
的车型中各随机抽取![]() 车,以
车,以![]() 表示这
表示这![]() 车中使用寿命不低于
车中使用寿命不低于![]() 年的车数,求
年的车数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)根据公司要求,采购成本由出租公司负责,平均每辆出租车每年上交公司![]() 万元,其余维修和保险等费用自理.假设每辆出租车的使用寿命都是整数年,用频率估计每辆出租车使用寿命的概率,分别以这
万元,其余维修和保险等费用自理.假设每辆出租车的使用寿命都是整数年,用频率估计每辆出租车使用寿命的概率,分别以这![]() 辆出租车所产生的平均利润作为决策依据,如果你是该公司的负责人,会选择采购哪款车型?
辆出租车所产生的平均利润作为决策依据,如果你是该公司的负责人,会选择采购哪款车型?
附: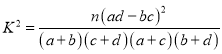 ,
,![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com