
分析 设P(x,y)为椭圆上的动点,由于椭圆方程可得-4≤x≤4.由|MP2=(x-m)2+y2=(x-m)2+12(1-$\frac{{x}^{2}}{16}$)=$\frac{1}{4}$(x-4m)2+12-3m2
,结合二次函数的性质及椭圆的性质可知,取得最小值4m≥4,结合点M在椭圆的长轴上,可求m得范围
解答 解:设P(x,y)为椭圆上的动点,由于椭圆方程为$\frac{x^2}{16}+\frac{y^2}{12}=1$,故-4≤x≤4.
|MP2=(x-m)2+y2=(x-m)2+12(1-$\frac{{x}^{2}}{16}$)=$\frac{1}{4}$(x-4m)2+12-3m2
∵当|MP|最小时,点P恰好落在椭圆的右顶点,即当x=4时,|MP|2取得最小值,而x∈[-4,4],
故有4m≥4,解得m≥1.
又点M在椭圆的长轴上,所以-4≤m≤4.故实数m的取值范围是[1,4].
故答案为:1≤m≤4.
点评 本本题主要考查了椭圆的性质的应用,解题中要注意椭圆的范围与二次函数的性质的应用是解决本题的关键.属于中档题.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
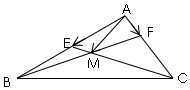 如图,在△ABC中,点E为AB边的中点,点F在AC边上,且CF=2FA,BF交CE于点M,设$\overrightarrow{AM}$=x$\overrightarrow{AE}$+y$\overrightarrow{AF}$,则x+y=$\frac{1}{5}$.
如图,在△ABC中,点E为AB边的中点,点F在AC边上,且CF=2FA,BF交CE于点M,设$\overrightarrow{AM}$=x$\overrightarrow{AE}$+y$\overrightarrow{AF}$,则x+y=$\frac{1}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4\sqrt{2}-7}{9}$ | B. | $\frac{-4\sqrt{2}-7}{9}$ | C. | $\frac{4-7\sqrt{2}}{9}$ | D. | $\frac{-4-7\sqrt{2}}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com