
【题目】已知函数f(x)=(2x-4)ex+a(x+2)2(x>0,a∈R,e是自然对数的底数).
(1)若f(x)是(0,+∞)上的单调递增函数,求实数a的取值范围;
(2)当a∈![]() 时,证明:函数f(x)有最小值,并求函数f(x)的最小值的取值范围.
时,证明:函数f(x)有最小值,并求函数f(x)的最小值的取值范围.
【答案】(1)![]() (2)(-2e,-2).
(2)(-2e,-2).
【解析】试题分析:(1)由题意得当x>0时,函数f′(x)≥0恒成立,再分离变量法转化为对应函数最值,根据导数求对应函数单调性,进而确定最值,得实数a的取值范围;(2)先研究导函数单调性,再根据零点存在定理得导函数有唯一一个零点,即为函数极小值点,也是最小值点,最后利用导数研究最小值函数单调性,即得最小值取值范围
试题解析:(1)f′(x)=2ex+(2x-4)ex+2a(x+2)=(2x-2)ex+2a(x+2),依题意,当x>0时,函数f′(x)≥0恒成立,即a≥-![]() 恒成立,记g(x)=-
恒成立,记g(x)=-![]() ,则g′(x)=-
,则g′(x)=-![]()
=-![]() <0,所以g(x)在(0,+∞)上单调递减,所以g(x)<g(0)=
<0,所以g(x)在(0,+∞)上单调递减,所以g(x)<g(0)=![]() ,所以a≥
,所以a≥![]() .
.
故a的取值范围为![]() .
.
(2)因为[f′(x)]′=2xex+2a>0,所以y=f′(x)是(0,+∞)上的增函数,又f′(0)=4a-2<0,f′(1)=6a>0,所以存在t∈(0,1)使得f′(t)=0,
又当x∈(0,t)时,f′(x)<0,当x∈(t,+∞)时,f′(x)>0,
所以当x=t时,f(x)min=f(t)=(2t-4)et+a(t+2)2.且有f′(t)=0a=-![]() ,
,
则f(x)min=f(t)=(2t-4)et-(t-1)(t+2)et=et(-t2+t-2),t∈(0,1).
记h(t)=et(-t2+t-2),则h′(t)=et(-t2+t-2)+et(-2t+1)=et(-t2-t-1)<0,
所以h(1)<h(t)<h(0),
即f(x)的最小值的取值范围是(-2e,-2).


科目:高中数学 来源: 题型:
【题目】已知圆C过点M(0,-2)、N(3,1),且圆心C在直线x+2y+1=0上.
(1)求圆C的方程;
(2)设直线ax-y+1=0与圆C交于A,B两点,是否存在实数a,使得过点P(2,0)的直线l垂直平分弦AB?若存在,求出实数a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(-![]() ,0),B(
,0),B(![]() ,0),直线MA,MB交于点M,它们的斜率之积为常数m(m≠0),且△MAB的面积最大值为
,0),直线MA,MB交于点M,它们的斜率之积为常数m(m≠0),且△MAB的面积最大值为![]() ,设动点M的轨迹为曲线E.
,设动点M的轨迹为曲线E.
(1)求曲线E的方程;
(2)过曲线E外一点Q作E的两条切线l1,l2,若它们的斜率之积为-1,那么![]() ·
·![]() 是否为定值?若是,请求出该值;若不是,请说明理由.
是否为定值?若是,请求出该值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着网络的发展,网上购物越来越受到人们的喜爱,各大购物网站为增加收入,促销策略越来越多样化,促销费用也不断增加.下表是某购物网站2017年1-8月促销费用(万元)和产品销量(万件)的具体数据.

(1)根据数据可知![]() 与
与![]() 具有线性相关关系,请建立
具有线性相关关系,请建立![]() 关于
关于![]() 的回归方程
的回归方程![]() (系数精确到
(系数精确到![]() );
);
(2)已知6月份该购物网站为庆祝成立1周年,特制定奖励制度:以![]() (单位:件)表示日销量,
(单位:件)表示日销量, ![]() ,则每位员工每日奖励100元;
,则每位员工每日奖励100元; ![]() ,则每位员工每日奖励150元;
,则每位员工每日奖励150元; ![]() ,则每位员工每日奖励200元.现已知该网站6月份日销量
,则每位员工每日奖励200元.现已知该网站6月份日销量![]() 服从正态分布
服从正态分布![]() ,请你计算某位员工当月奖励金额总数大约多少元.(当月奖励金额总数精确到百分位)
,请你计算某位员工当月奖励金额总数大约多少元.(当月奖励金额总数精确到百分位)
参考数据: ![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() 分别为第
分别为第![]() 个月的促销费用和产品销量,
个月的促销费用和产品销量, ![]() .
.
参考公式:
(1)对于一组数据![]() ,
, ![]() ,
, ![]() ,
, ![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为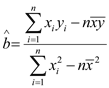 ,
, ![]() .
.
(2)若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心
的圆心![]() 在抛物线
在抛物线![]() 上,圆
上,圆![]() 过原点且与抛物线的准线相切.
过原点且与抛物线的准线相切.
(1)求该抛物线的方程;
(2)过抛物线焦点![]() 的直线
的直线![]() 交抛物线于
交抛物线于![]() ,
, ![]() 两点,分别在点
两点,分别在点![]() ,
, ![]() 处作抛物线的两条切线交于
处作抛物线的两条切线交于![]() 点,求三角形
点,求三角形![]() 面积的最小值及此时直线
面积的最小值及此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在图所示的五面体中,面ABCD为直角梯形,![]() ,平面
,平面![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,
,![]() 是边长为2的正三角形.
是边长为2的正三角形.

![]() 证明:
证明:![]() 平面ACF;
平面ACF;
![]() 若点P在线段EF上,且二面角
若点P在线段EF上,且二面角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (k为常数,e=2.718 28…是自然对数的底数).
(k为常数,e=2.718 28…是自然对数的底数).
(1)当k≤0时,求函数f (x)的单调区间;
(2)若函数f (x)在(0,2)内存在两个极值点,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com