
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 吋,解不等式
吋,解不等式![]() ;
;
(2)设![]() .
.
①当![]() 时,若存在
时,若存在![]() ,使得
,使得![]() ,证明:
,证明:![]() ;
;
②当![]() 时,讨论
时,讨论![]() 的零点个数.
的零点个数.
【答案】(1)![]() (2)①见解析②见解析
(2)①见解析②见解析
【解析】
(1)将![]() 代入,不妨设
代入,不妨设![]() ,利用导数判断函数单调递增,由
,利用导数判断函数单调递增,由![]() ,即可求解.
,即可求解.
(2)①由![]() ,代入解析式整理可得
,代入解析式整理可得![]() ,由
,由![]() ,利用基本不等式可得
,利用基本不等式可得![]() ,方法一:设
,方法一:设![]() ,利用导数即可证出;方法二:利用反证法,假设
,利用导数即可证出;方法二:利用反证法,假设![]() ,找出
,找出![]() ,与已知矛盾即可. ②
,与已知矛盾即可. ②![]() ,求导函数
,求导函数![]() ,求出函数的单调区间以及最值,且
,求出函数的单调区间以及最值,且![]() ,讨论
,讨论![]() 、
、![]() 或
或![]() 即可得出零点个数.
即可得出零点个数.
解:(1)设![]() ,
,
则 ,
,
所以![]() 在
在![]() 上递增,又
上递增,又![]() ,所以
,所以![]() ,
,
所以![]() 的解集为
的解集为![]() .
.
(2)①证明:由![]() 得
得![]() ,
,
即![]() ,又
,又![]() ,
,
所以![]() ,
,
因为![]() ,所以“
,所以“![]() ”不成立.
”不成立.
思路一:
设![]() ,
,![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 单调递减,
单调递减,
又![]() ,所以
,所以![]() ,即
,即![]() .
.
思路二:
假设![]() ,则
,则![]() ,
,![]() ,所以
,所以![]() ,
,
这与![]() 矛盾,故
矛盾,故![]() .
.
②![]() ,
,
当![]() 时,
时,![]() ,
,
令![]() 得
得![]() (负值舍去).
(负值舍去).
所以当 时,
时,![]() ,
,![]() 为减函数,
为减函数,
当 时,
时,![]() ,
,![]() 为增函数.
为增函数.
又![]() .
.
![]() 当
当![]() ,即
,即![]() 时,
时,![]() 有一个零点.
有一个零点.
![]() 当
当![]() ,即
,即![]() 时,由
时,由![]() 可知
可知 ,
,
又![]() ,且
,且![]() ,
,
所以,![]() 在
在![]() 有一个零点,故此时
有一个零点,故此时![]() 有两个零点;
有两个零点;
![]() 当
当![]() ,即
,即![]() 时,由
时,由![]() 可知
可知 ,
,
令![]() ,则
,则![]() ,
,
所以当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减,所以
单调递减,所以![]() ,
,
故![]() ,则
,则![]() .
.
所以![]() ,所以
,所以![]() ,且
,且![]() ,
,
所以,![]() 在
在![]() 有一个零点,故此时
有一个零点,故此时![]() 有两个零点.
有两个零点.
综上,当![]() 时,
时,![]() 有1个零点;
有1个零点;
当![]() 且
且![]() 时,
时,![]() 有2个零点.
有2个零点.


科目:高中数学 来源: 题型:
【题目】在三棱柱ABC﹣A1B1C1中,M,M1分别为AB,A1B1中点.
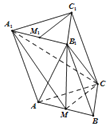
(1)求证:C1M1∥面A1MC;
(2)若面ABC⊥面ABB1A1,△AB1B为正三角形,AB=2,BC=1,![]() ,求四棱锥B1﹣AA1C1C的体积.
,求四棱锥B1﹣AA1C1C的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+acosx.
(1)求函数f(x)的奇偶性.并证明当|a|≤2时函数f(x)只有一个极值点;
(2)当a=π时,求f(x)的最小值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把4个相同的小球全部放入2个不同的盒子里,每个盒子至少放1个球,不同的放法数记为![]() ;把4个不同的小球全部放入2个不同的盒子里,每个盒子至少放1个球,不同的放法数记为
;把4个不同的小球全部放入2个不同的盒子里,每个盒子至少放1个球,不同的放法数记为![]() .现在从
.现在从![]() 到
到![]() 的所有整数中(包括
的所有整数中(包括![]() 和
和![]() 两个整数)抽取3个数,则这3个数之和共有( )种结果.
两个整数)抽取3个数,则这3个数之和共有( )种结果.
A.26B.27C.28D.29
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,上顶点为A,过
,上顶点为A,过![]() 的直线
的直线![]() 与y轴交于点M,满足
与y轴交于点M,满足![]() (O为坐标原点),且直线l与直线
(O为坐标原点),且直线l与直线![]() 之间的距离为
之间的距离为![]() .
.
(1)求椭圆C的方程;
(2)在直线![]() 上是否存在点P,满足
上是否存在点P,满足![]() ?存在,指出有几个这样的点(不必求出点的坐标);若不存在,请说明理由.
?存在,指出有几个这样的点(不必求出点的坐标);若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在抗击新冠肺炎疫情期间,很多人积极参与了疫情防控的志愿者活动.各社区志愿者服务类型有:现场值班值守,社区消毒,远程教育宣传,心理咨询(每个志愿者仅参与一类服务).参与A,B,C三个社区的志愿者服务情况如下表:
社区 | 社区服务总人数 | 服务类型 | |||
现场值班值守 | 社区消毒 | 远程教育宣传 | 心理咨询 | ||
A | 100 | 30 | 30 | 20 | 20 |
B | 120 | 40 | 35 | 20 | 25 |
C | 150 | 50 | 40 | 30 | 30 |
(1)从上表三个社区的志愿者中任取1人,求此人来自于A社区,并且参与社区消毒工作的概率;
(2)从上表三个社区的志愿者中各任取1人调查情况,以X表示负责现场值班值守的人数,求X的分布列;
(3)已知A社区心理咨询满意率为0.85,B社区心理咨询满意率为0.95,C社区心理咨询满意率为0.9,“![]() ,
,![]() ,
,![]() ”分别表示A,B,C社区的人们对心理咨询满意,“
”分别表示A,B,C社区的人们对心理咨询满意,“![]() ,
,![]() ,
,![]() ”分别表示A,B,C社区的人们对心理咨询不满意,写出方差
”分别表示A,B,C社区的人们对心理咨询不满意,写出方差![]() ,
,![]() ,
,![]() 的大小关系.(只需写出结论)
的大小关系.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】11月,2019全国美丽乡村篮球大赛在中国农村改革的发源地-安徽凤阳举办,其间甲、乙两人轮流进行篮球定点投篮比赛(每人各投一次为一轮),在相同的条件下,每轮甲乙两人在同一位置,甲先投,每人投一次球,两人有1人命中,命中者得1分,未命中者得-1分;两人都命中或都未命中,两人均得0分,设甲每次投球命中的概率为![]() ,乙每次投球命中的概率为
,乙每次投球命中的概率为![]() ,且各次投球互不影响.
,且各次投球互不影响.
(1)经过1轮投球,记甲的得分为![]() ,求
,求![]() 的分布列;
的分布列;
(2)若经过![]() 轮投球,用
轮投球,用![]() 表示经过第
表示经过第![]() 轮投球,累计得分,甲的得分高于乙的得分的概率.
轮投球,累计得分,甲的得分高于乙的得分的概率.
①求![]() ;
;
②规定![]() ,经过计算机计算可估计得
,经过计算机计算可估计得![]() ,请根据①中
,请根据①中![]() 的值分别写出a,c关于b的表达式,并由此求出数列
的值分别写出a,c关于b的表达式,并由此求出数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线C:![]() ,过抛物线焦点F的直线交抛物线C于A,B两点,P是抛物线外一点,连接
,过抛物线焦点F的直线交抛物线C于A,B两点,P是抛物线外一点,连接![]() ,
,![]() 分别交抛物线于点C,D,且
分别交抛物线于点C,D,且![]() ,设
,设![]() ,
,![]() 的中点分别为M,N.
的中点分别为M,N.
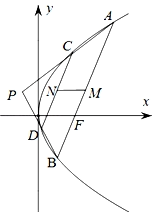
(1)求证:![]() 轴;
轴;
(2)若![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com