
【题目】如图,在直三棱柱ABC﹣A1B1C1中,底面△ABC是等腰直角三角形,且斜边 ![]() ,侧棱AA1=2,点D为AB的中点,点E在线段AA1上,AE=λAA1(λ为实数).
,侧棱AA1=2,点D为AB的中点,点E在线段AA1上,AE=λAA1(λ为实数).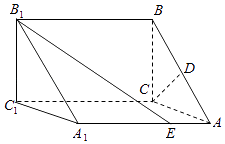
(1)求证:不论λ取何值时,恒有CD⊥B1E;
(2)当 ![]() 时,记四面体C1﹣BEC的体积为V1 , 四面体D﹣BEC的体积为V2 , 求V1:V2 .
时,记四面体C1﹣BEC的体积为V1 , 四面体D﹣BEC的体积为V2 , 求V1:V2 .
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 存在互不相等实数a,b,c,d,有f(a)=f(b)=f(c)=f(d)=m.现给出三个结论:
存在互不相等实数a,b,c,d,有f(a)=f(b)=f(c)=f(d)=m.现给出三个结论:
⑴m∈[1,2);
⑵a+b+c+d∈[e﹣3+e﹣1﹣2,e﹣4﹣1),其中e为自然对数的底数;
⑶关于x的方程f(x)=x+m恰有三个不等实根.
正确结论的个数为( )
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( )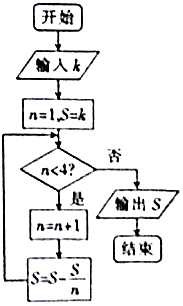
A.4.5
B.6
C.7.5
D.9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC中,AC=2,A=120°, ![]() .
.
(Ⅰ)求边AB的长;
(Ⅱ)设(3,4)是BC边上一点,且△ACD的面积为 ![]() ,求∠ADC的正弦值.
,求∠ADC的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f'(x)=2x+m,且f(0)=0,函数f(x)的图象在点A(1,f(1))处的切线的斜率为3,数列 ![]() 的前n项和为Sn , 则S2017的值为( )
的前n项和为Sn , 则S2017的值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C1:x2+y2=r2(r>0)与直线l0:y= ![]() 相切,点A为圆C1上一动点,AN⊥x轴于点N,且动点M满足
相切,点A为圆C1上一动点,AN⊥x轴于点N,且动点M满足 ![]() ,设动点M的轨迹为曲线C.
,设动点M的轨迹为曲线C.
(1)求动点M的轨迹曲线C的方程;
(2)若直线l与曲线C相交于不同的两点P、Q且满足以PQ为直径的圆过坐标原点O,求线段PQ长度的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等腰梯形ABCD中AB∥CD,AB=2CD=4,∠BAD=60°,双曲线以A,B为焦点,且与线段CD(包括端点C、D)有两个交点,则该双曲线的离心率的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,
, ![]() .
.
(1)求函数 ![]() 的单调增区间;
的单调增区间;
(2)若 ![]() ,解不等式
,解不等式 ![]() ;
;
(3)若 ![]() ,且对任意
,且对任意 ![]() ,方程
,方程 ![]() 在
在 ![]() 总存在两不相等的实数根,求
总存在两不相等的实数根,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com