
【题目】已知椭圆![]() 过点
过点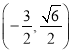 ,顺次连接椭圆的四个顶点得到的四边形的面积为
,顺次连接椭圆的四个顶点得到的四边形的面积为![]() ,点
,点![]() .
.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)已知点![]() ,是椭圆
,是椭圆![]() 上的两点.
上的两点.
(ⅰ)若![]() ,且
,且![]() 为等边三角形,求
为等边三角形,求![]() 的面积;
的面积;
(ⅱ)若![]() ,证明:
,证明: ![]() 不可能为等边三角形.
不可能为等边三角形.
【答案】(I)![]() ;(II)详见解析.
;(II)详见解析.
【解析】试题分析:(Ⅰ)根据面积公式得到![]() ,以及点在曲线上,代入得到
,以及点在曲线上,代入得到![]() ,以及
,以及![]() ,求得
,求得![]() ;(Ⅱ)(ⅰ)根据等边三角形的性质,可得直线
;(Ⅱ)(ⅰ)根据等边三角形的性质,可得直线![]() 的倾斜角是
的倾斜角是![]() 或
或![]() ,这样求得直线
,这样求得直线![]() 的方程,联立椭圆方程,得到点
的方程,联立椭圆方程,得到点![]() 的坐标,求得面积;(ⅱ)因为
的坐标,求得面积;(ⅱ)因为![]() ,所以斜率存在,设直线
,所以斜率存在,设直线![]() 的方程是
的方程是![]() ,与椭圆方程联立,得到根与系数的关系,并且表示线段
,与椭圆方程联立,得到根与系数的关系,并且表示线段![]() 中点
中点![]() 的坐标,若是等边三角形,则
的坐标,若是等边三角形,则![]() ,可求得
,可求得![]() ,不合题意.
,不合题意.
试题解析:(Ⅰ)依题意, ![]() ,
, ![]() ,联立两式,解得
,联立两式,解得![]() ,
, ![]() ,故椭圆
,故椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)(ⅰ)由![]() 且
且![]() 为等边三角形及椭圆的对称性可知,直线
为等边三角形及椭圆的对称性可知,直线![]() 和直线
和直线![]() 与
与![]() 轴的夹角为
轴的夹角为![]() ,由
,由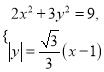 可得
可得![]() .
.
即![]() 或
或![]() ,当
,当![]() 时,
时, ![]() 的面积为
的面积为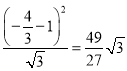 ;
;
当![]() 时,
时, ![]() 的面积为
的面积为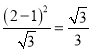 .
.
(ⅱ)因为![]() ,故直线
,故直线![]() 斜率存在,设直线
斜率存在,设直线![]() ,
, ![]() 中点为
中点为![]() ,联立
,联立![]() 消去
消去![]() 得,
得, ![]()
由![]() 得到
得到![]() ,①
,①
所以![]() ,
, ![]() ,
,
所以![]() .
.
又![]() ,若
,若![]() 为等边三角形,则有
为等边三角形,则有![]() ,
,
即![]() ,即
,即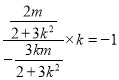 ,化简得
,化简得![]() ,②
,②
由②得点![]() 横坐标为
横坐标为![]() ,不合题意.
,不合题意.
故![]() 不可能为等边三角形.
不可能为等边三角形.
(用点差法求![]() 点坐标也可)
点坐标也可)


科目:高中数学 来源: 题型:
【题目】已知数列![]() ,
, ![]() 都是单调递增数列,若将这两个数列的项按由小到大的顺序排成一列(相同的项视为一项),则得到一个新数列
都是单调递增数列,若将这两个数列的项按由小到大的顺序排成一列(相同的项视为一项),则得到一个新数列![]() .
.
(1)设数列![]() 、
、![]() 分别为等差、等比数列,若
分别为等差、等比数列,若![]() ,
, ![]() ,
, ![]() ,求
,求![]() ;
;
(2)设![]() 的首项为1,各项为正整数,
的首项为1,各项为正整数, ![]() ,若新数列
,若新数列![]() 是等差数列,求数列
是等差数列,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)设![]() (
(![]() 是不小于2的正整数),
是不小于2的正整数),![]() ,是否存在等差数列
,是否存在等差数列![]() ,使得对任意的
,使得对任意的![]() ,在
,在![]() 与
与![]() 之间数列
之间数列![]() 的项数总是
的项数总是![]() ?若存在,请给出一个满足题意的等差数列
?若存在,请给出一个满足题意的等差数列![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代著名数学经典.其中对勾股定理的论术比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深1寸,锯道长1尺.问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示(阴影部分为镶嵌在墙体内的部分).已知弦![]() 尺,弓形高
尺,弓形高![]() 寸,估算该木材镶嵌在墙中的体积约为( )
寸,估算该木材镶嵌在墙中的体积约为( )
(注:1丈=10尺=100寸, ![]() ,
, ![]() )
)

A. 633立方寸 B. 620立方寸 C. 610立方寸 D. 600立方寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,M、N、K分别是正方体ABCD﹣A1B1C1D1的棱AB,CD,C1D1的中点.求证:
(1)AN∥平面A1MK;
(2)MK⊥平面A1B1C.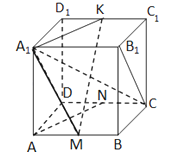
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】服装厂拟在2017年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)![]() 万件与年促销费用
万件与年促销费用![]() (
(![]() )万元满足
)万元满足![]() .已知
.已知![]() 年生产该产品的固定投入为
年生产该产品的固定投入为![]() 万元,每生产
万元,每生产![]() 万件该产品需要投入
万件该产品需要投入![]() 万元.厂家将每件产品的销售价格定为每件产品年平均成本的
万元.厂家将每件产品的销售价格定为每件产品年平均成本的![]() 倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).
倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).
(1)将2017年该产品的利润![]() 万元表示为年促销费用
万元表示为年促销费用![]() 万元的函数;
万元的函数;
(2)该服装厂2017年的促销费用投入多少万元时,利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到直线
到直线![]() 的距离是它到点
的距离是它到点![]() 的距离的
的距离的![]() 倍.
倍.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设轨迹![]() 上一动点
上一动点![]() 满足:
满足: ![]() ,其中
,其中![]() 是轨迹
是轨迹![]() 上的点,且直线
上的点,且直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() ,若
,若![]() 为一动点,
为一动点, 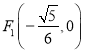 ,
, 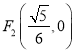 为两定点,求
为两定点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面为平行四边形的四棱锥P﹣ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.
(Ⅰ)求证:AC⊥PB;
(Ⅱ)求证:PB∥平面AEC.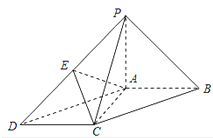
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com