
【题目】如图,一段南北两岸互相平行、宽度为![]() 的景观河.靠南岸水域有一半径为
的景观河.靠南岸水域有一半径为![]() 半圆形亲水平台,圆心
半圆形亲水平台,圆心![]() 在南岸边上,北岸边有一风雨亭
在南岸边上,北岸边有一风雨亭![]() (底座大小忽略不计),风雨亭
(底座大小忽略不计),风雨亭![]() 距位于北岸边上的
距位于北岸边上的![]() 点
点![]() (
(![]() 在
在![]() 的正北方,
的正北方,![]() 在
在![]() 的右侧).为了方便市民休闲,现决定修建折线型步行栈道
的右侧).为了方便市民休闲,现决定修建折线型步行栈道![]() (图中粗线所示),其中
(图中粗线所示),其中![]() 与圆
与圆![]() 相切,
相切,![]() 段的造价为4万元/
段的造价为4万元/![]() ,
,![]() 段和
段和![]() 段分别在南北两岸边上(其中
段分别在南北两岸边上(其中![]() 为半圆
为半圆![]() 的一条直径的左端点),
的一条直径的左端点),![]() 段和
段和![]() 段的造价都为2万元/
段的造价都为2万元/![]() .记
.记![]() 为
为![]() ,
,![]() .
.
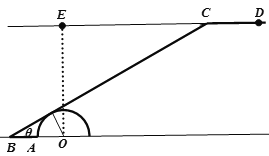
(1)若![]() ,求栈道
,求栈道![]() 段的长;
段的长;
(2)设三段栈道总造价为![]() ,求
,求![]() 的最小值.
的最小值.
科目:高中数学 来源: 题型:
【题目】记![]() 表示m,n中的最大值,如
表示m,n中的最大值,如![]() .已知函数
.已知函数![]() ,
,![]() .
.
(1)设![]() ,求函数
,求函数![]() 在
在![]() 上的零点个数;
上的零点个数;
(2)试探讨是否存在实数![]() ,使得
,使得![]() 对
对![]() 恒成立?若存在,求a的取值范围;若不存在,说明理由.
恒成立?若存在,求a的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,直线l:x+2y=4与椭圆有且只有一个交点T.
,直线l:x+2y=4与椭圆有且只有一个交点T.
(I)求椭圆C的方程和点T的坐标;
(Ⅱ)O为坐标原点,与OT平行的直线l′与椭圆C交于不同的两点A,B,直线l′与直线l交于点P,试判断![]() 是否为定值,若是请求出定值,若不是请说明理由.
是否为定值,若是请求出定值,若不是请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 设椭圆![]() 的左焦点为
的左焦点为![]() ,左顶点为
,左顶点为![]() ,顶点为B.已知
,顶点为B.已知![]() (
(![]() 为原点).
为原点).
(Ⅰ)求椭圆的离心率;
(Ⅱ)设经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆在
与椭圆在![]() 轴上方的交点为
轴上方的交点为![]() ,圆
,圆![]() 同时与
同时与![]() 轴和直线
轴和直线![]() 相切,圆心
相切,圆心![]() 在直线
在直线![]() 上,且
上,且![]() ,求椭圆的方程.
,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】本小题满分13分)
工作人员需进入核电站完成某项具有高辐射危险的任务,每次只派一个人进去,且每个人只派一次,工作时间不超过10分钟,如果有一个人10分钟内不能完成任务则撤出,再派下一个人.现在一共只有甲、乙、丙三个人可派,他们各自能完成任务的概率分别![]()
![]() ,假设
,假设![]() 互不相等,且假定各人能否完成任务的事件相互独立.
互不相等,且假定各人能否完成任务的事件相互独立.
(1)如果按甲在先,乙次之,丙最后的顺序派人,求任务能被完成的概率.若改变三个人被派出的先后顺序,任务能被完成的概率是否发生变化?
(2)若按某指定顺序派人,这三个人各自能完成任务的概率依次为![]() ,其中
,其中![]() 是
是![]() 的一个排列,求所需派出人员数目
的一个排列,求所需派出人员数目![]() 的分布列和均值(数字期望)
的分布列和均值(数字期望)![]() ;
;
(3)假定![]() ,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的均值(数字期望)达到最小.
,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的均值(数字期望)达到最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业积极响应国家“科技创新”的号召,大力研发人工智能产品,为了对一批新研发的产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据![]()
![]() ,如下表所示:
,如下表所示:
试销单价 | 1 | 2 | 3 | 4 | 5 | 6 |
产品销量 | 91 | 86 |
| 78 | 73 | 70 |
附:参考公式: ,
,![]() ,
,
参考数据:![]() ,
,![]() ,
,![]() .
.
(1)求![]() 的值;
的值;
(2)已知变量![]() ,
,![]() 具有线性相关关系,求产品销量
具有线性相关关系,求产品销量![]() (件)关于试销单价
(件)关于试销单价![]() (百元)的线性回归方程
(百元)的线性回归方程![]() (计算结果精确到整数位);
(计算结果精确到整数位);
(3)用![]() 表示用正确的线性回归方程得到的与
表示用正确的线性回归方程得到的与![]() 对应的产品销量的估计值.当销售数据
对应的产品销量的估计值.当销售数据![]() 的残差的绝对值
的残差的绝对值![]() 时,则将销售数据称为一个“有效数据”.现从这6组销售数据中任取2组,求抽取的2组销售数据都是“有效数据”的概率.
时,则将销售数据称为一个“有效数据”.现从这6组销售数据中任取2组,求抽取的2组销售数据都是“有效数据”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com