
 的展开式的各项系数之和为M,二项式系数之和为N,若M+N=16,则展开式中的常数项为 .
的展开式的各项系数之和为M,二项式系数之和为N,若M+N=16,则展开式中的常数项为 .  中令x=1可得M,由二项式系数的性质可得N,又由题意M+N=16可得2n=16,解可得n的值,再根据二项式定理可得(x-
中令x=1可得M,由二项式系数的性质可得N,又由题意M+N=16可得2n=16,解可得n的值,再根据二项式定理可得(x-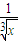 )4的展开式的通项,令x的系数为0可得r的值,将r的值代入可得通项可得其常数项,即可得答案.
)4的展开式的通项,令x的系数为0可得r的值,将r的值代入可得通项可得其常数项,即可得答案. 的展开式的各项系数之和为M,
的展开式的各项系数之和为M, 中令x=1可得,M=(1-1)n=0
中令x=1可得,M=(1-1)n=0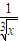 )4的展开式的通项为Tr+1=C4r(x)4-r•(-
)4的展开式的通项为Tr+1=C4r(x)4-r•(- )r=(-1)r•C4r•
)r=(-1)r•C4r• ,
, =0,可得r=3,
=0,可得r=3,

科目:高中数学 来源:2014届陕西省高二下学期期末考试理科数学试卷(解析版) 题型:填空题
设 的展开式的各项系数之和为
的展开式的各项系数之和为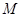 ,二项式系数之和为
,二项式系数之和为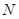 ,若
,若 ,则展开式中常数项为___________.
,则展开式中常数项为___________.
查看答案和解析>>
科目:高中数学 来源:2014届湖南省高二4月段考数学理科试卷(解析版) 题型:选择题
设 的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n为(
)
的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n为(
)
A.4 B.5 C.6 D.8
查看答案和解析>>
科目:高中数学 来源:2011-2012学年安徽省安庆市高三第二次模拟考试理科数学试卷(解析版) 题型:填空题
设 的展开式的各项系数之和为M,二项式系数之和为N,若M,8,N三数成等比数列,则展开式中第四项为____
的展开式的各项系数之和为M,二项式系数之和为N,若M,8,N三数成等比数列,则展开式中第四项为____
查看答案和解析>>
科目:高中数学 来源:山东省济宁市2012届高二下学期期末考试理科数学 题型:选择题
设 的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n为( )
的展开式的各项系数的和为P,所有二项式系数的和为S,若P+S=272,则n为( )
A.4 B.5 C.6 D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com