考点:命题的真假判断与应用
专题:简易逻辑
分析:A,写出命题“对?x∈R,都有x
2≥0”的否定,可判断A;
B,利用充分必要条件的概念,通过举例说明可判断B;
C,利用“原命题与其逆否命题真假性一致”可判断“若tanα≠
,则α≠
”的逆否命题为真,从而可判断C;
D,依题意可知,命题“至少有一位学生不及格”可表示为(¬p)∨(¬q),可判断D.
解答:
解:A,命题“对?x∈R,都有x
2≥0”的否定为“?x
0∈R,使得x
02<0”,A正确;
B,“a>b”不能⇒“ac
2>bc
2”,例如c=0时ac
2>bc
2就不成立,即充分性不成立;反之,“ac
2>bc
2”⇒“a>b”,即必要性成立,B正确;
C,“若tanα≠
,则α≠
”其逆否命题为“若α=
,则tanα=
”是真命题,由“原命题与其逆否命题真假性一致”可知,C正确;
D,甲、乙两位学生参与数学模拟考试,设命题p是“甲考试及格”,q是“乙考试及格”,则命题“至少有一位学生不及格”可表示为(¬p)∨(¬q),而不是(¬p)∧(¬q),D错误;
故选:D.
点评:本题考查命题的真假判断与应用,综合考查命题的否定、充分必要条件的理解与应用,考查四种命题之间的关系与复合命题的真假判断,属于中档题.



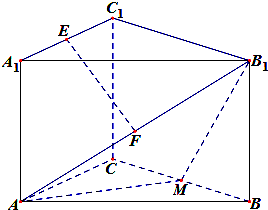 在正三棱柱ABC-A1B1C1中,BC=
在正三棱柱ABC-A1B1C1中,BC=