
【题目】△ABC中内角A、B、C的对边分别为a、b、c,且2acosC=2b﹣c.
(Ⅰ)求角A的大小;
(Ⅱ)如果a=1,求b+c的取值范围.
【答案】解:(Ⅰ)2acosC=2b﹣c,由正弦定理可得:sinAcosC+ ![]() sinC=sinB, sinB=sin(A+C)=sinAcosC+cosAsinC.∴
sinC=sinB, sinB=sin(A+C)=sinAcosC+cosAsinC.∴ ![]() sinC=cosAsinC,∵sinC≠0,
sinC=cosAsinC,∵sinC≠0,
∴cosA= ![]() ,
,
角A的大小为: ![]() ;
;
(Ⅱ)由正弦定理可得:b= ![]() ,
, ![]() ,
,
∴b+c= ![]() =
= ![]() =
= 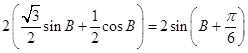 ,
,
∵ ![]() ∴
∴ ![]() ,
,
∴ ![]() ∈
∈ ![]() ,
,
∴ ![]() ,
,
∴b+c的取值范围:(1,2].
【解析】(Ⅰ)利用正弦定理以及两角和与差的三角函数,化简方程,即可求角A的余弦值,得到A的值;(Ⅱ)利用正弦定理区别b,c的值,b+c为B的正弦函数,通过三角函数值域,求出b+c的取值范围.
【考点精析】根据题目的已知条件,利用正弦定理的定义和余弦定理的定义的相关知识可以得到问题的答案,需要掌握正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() .
.


科目:高中数学 来源: 题型:
【题目】某高校大一新生中的6名同学打算参加学校组织的“演讲团”、“吉他协会”等五个社团,若每名同学必须参加且只能参加1个社团且每个社团至多两人参加,则这6个人中没有人参加“演讲团”的不同参加方法数为( )
A. 3600 B. 1080 C. 1440 D. 2520
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个透明密闭的正方体容器中,恰好盛有该容器一半容积的水,任意转动这个正方体,则水面在容器中的形状可以是:
①三角形;②矩形;③正方形;④正六边形.
其中正确的结论是(把你认为正确的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,C是圆O上不同于A,B的一点,PA⊥平面ABC,E是PC的中点, ![]() ,PA=AC=1.
,PA=AC=1. 
(1)求证:AE⊥PB;
(2)求二面角A﹣PB﹣C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线y=Asin(wx+φ)(A>0,w>0)上的一个最高点的坐标为( ![]() ,
, ![]() ),由此点到相邻最低点间的曲线与x轴交于点(
),由此点到相邻最低点间的曲线与x轴交于点( ![]() π,0),φ∈(﹣
π,0),φ∈(﹣ ![]() ,
, ![]() ).
).
(1)求这条曲线的函数解析式;
(2)求函数的单调增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图⑴、⑵、⑶、⑷为四个几何体的三视图,根据三视图可以判断这四个几何体依次分别为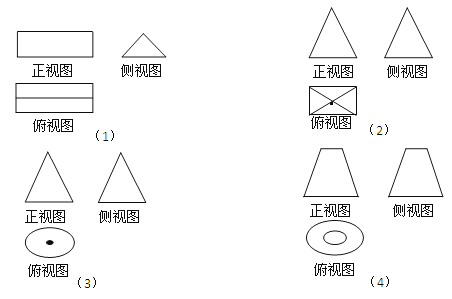
A.三棱台、三棱柱、圆锥、圆台
B.三棱台、三棱锥、圆锥、圆台
C.三棱柱、正四棱锥、圆锥、圆台
D.三棱柱、三棱台、圆锥、圆台
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且Sn=4an﹣3(n∈N*).
(Ⅰ)证明:数列{an}是等比数列;
(Ⅱ)若数列{bn}满足bn+1=an+bn(n∈N*),且b1=2,求数列{bn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=sin2x的图象向左平移 ![]() 个单位,再向上平移1个单位,所得图象的函数解析式是( )
个单位,再向上平移1个单位,所得图象的函数解析式是( )
A.y=cos2x
B.y=2cos2x
C.![]()
D.y=2sin2x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2﹣3x,则函数g(x)=f(x)﹣x+3的零点的集合为( )
A.{1,3}
B.{﹣3,﹣1,1,3}
C.{2﹣ ![]() ,1,3}
,1,3}
D.{﹣2﹣ ![]() ,1,3}
,1,3}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com