
分析 (1)根据一次函数的性质求出集合A,根据对数函数的性质求出集合B即可;(2)求出A∩B,结合f(x)的单调性求出f(x)的值域即可.
解答 解:(1)∵集合A={a|一次函数y=(4a-1)x+b在R上是增函数},
∴4a-1>0,解得:a>$\frac{1}{4}$,
故$A=(\frac{1}{4},+∞)$…(1分),
由$log_a^{\;}\frac{3}{4}<1$得:
当0<a<1时,loga$\frac{3}{4}$<1=logaa,解得:0<a<$\frac{3}{4}$,
当a>1时,loga$\frac{3}{4}$<1=logaa,解得:a>$\frac{3}{4}$,而a>1,故a>1,
∴$B=(0,\frac{3}{4})∪(1,+∞)$…(6分)
(2)$A∩C=(\frac{1}{4},\frac{3}{4})$…(7分)
∵函数y=x在(0,+∞)是增函数,
$y=\frac{1}{x}$在(0,+∞)上是减函数,
∴$f(x)=x-\frac{1}{x}$在(0,+∞)是增函数 …(9分)
所以当$x∈(\frac{1}{4},\frac{3}{4})$时…(12分)
有$-\frac{15}{4}=f(\frac{1}{4})<f(x)<f(\frac{3}{4})=-\frac{7}{12}$…(11分)
即函数$f(x)=x-\frac{1}{x}$的值域是$(-\frac{15}{4},-\frac{7}{12})$…(12分)
点评 本题考查了函数的单调性、最值问题,考查对数函数的性质以及集合的运算,是一道中档题.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示,O是坐标原点,两个正方形OABC、BDEF的顶点中,O、A、C、D、F五个点都在抛物线y2=2px(p>0)上,另外,B、E两个点都在x轴上,若这两个正方形的面积之和为10,则( )
如图所示,O是坐标原点,两个正方形OABC、BDEF的顶点中,O、A、C、D、F五个点都在抛物线y2=2px(p>0)上,另外,B、E两个点都在x轴上,若这两个正方形的面积之和为10,则( )| A. | p=1 | B. | p=2 | C. | p=$\frac{1}{2}$ | D. | p=$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
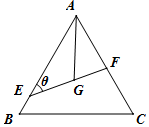 如图所示,△ABC是边长为6的等边三角形,G是它的重心(三条中线的交点),过G的直线分别交线段AB、AC于E、F两点,∠AEG=θ.
如图所示,△ABC是边长为6的等边三角形,G是它的重心(三条中线的交点),过G的直线分别交线段AB、AC于E、F两点,∠AEG=θ.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在直四棱柱(侧棱与底面垂直的四棱柱)ABCD-A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC,给出以下结论:
如图,在直四棱柱(侧棱与底面垂直的四棱柱)ABCD-A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC,给出以下结论:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜欢吃辣 | 不喜欢吃辣 | 合计 | |
| 男生 | 40 | 10 | 50 |
| 女生 | 20 | 30 | 50 |
| 合计 | 60 | 40 | 100 |
| p(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com