
【题目】已知抛物线 ![]() 上的一点
上的一点 ![]() 的横坐标为
的横坐标为 ![]() ,焦点为
,焦点为 ![]() ,且
,且 ![]() ,直线
,直线 ![]() 与抛物线
与抛物线 ![]() 交于
交于 ![]() 两点.
两点.
(1)求抛物线 ![]() 的方程;
的方程;
(2)若 ![]() 是
是 ![]() 轴上一点,且△
轴上一点,且△ ![]() 的面积等于
的面积等于 ![]() ,求点
,求点 ![]() 的坐标.
的坐标.
【答案】
(1)解:依题意得 ![]() ,所以
,所以 ![]() ,所以抛物线方程为
,所以抛物线方程为 ![]()
(2)解:设 ![]() ,联立得方程组
,联立得方程组 ![]()
消去 ![]() 得
得 ![]() ,从而
,从而 ![]()
由弦长公式得 ![]() ,
,
设 ![]() ,
, ![]() 到直线
到直线 ![]() 的距离为
的距离为 ![]() ,则
,则 ![]() ,
,
又 ![]() ,则
,则 ![]() ,所以
,所以 ![]()
![]() 或
或 ![]() ,故点
,故点 ![]() 坐标为
坐标为 ![]() 或
或 ![]()
【解析】(1) 根据题意利用抛物线上的点的几何意义可求出 ![]() + 3 = 4,求出P的值进而得出抛物线的方程。(2)首先设出了两个点的坐标然后联立直线和抛物线的方程消元可得到关于y的方程,借助韦达定理求出两根之和以及两根之积,代入两点间的距离公式求出弦长 | A B |的值,再由点到直线的距离公式求出三角形的高线的值,代入到三角形的面积公式的关于a的式子求出a的值进而得到点P的坐标。
+ 3 = 4,求出P的值进而得出抛物线的方程。(2)首先设出了两个点的坐标然后联立直线和抛物线的方程消元可得到关于y的方程,借助韦达定理求出两根之和以及两根之积,代入两点间的距离公式求出弦长 | A B |的值,再由点到直线的距离公式求出三角形的高线的值,代入到三角形的面积公式的关于a的式子求出a的值进而得到点P的坐标。
【考点精析】解答此题的关键在于理解抛物线的定义的相关知识,掌握平面内与一个定点![]() 和一条定直线
和一条定直线![]() 的距离相等的点的轨迹称为抛物线.定点
的距离相等的点的轨迹称为抛物线.定点![]() 称为抛物线的焦点,定直线
称为抛物线的焦点,定直线![]() 称为抛物线的准线.
称为抛物线的准线.


科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系.
(1)将直线l: 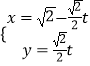 (t为参数)化为极坐标方程;
(t为参数)化为极坐标方程;
(2)设P是(1)中直线l上的动点,定点A( ![]() ,
, ![]() ),B是曲线ρ=﹣2sinθ上的动点,求|PA|+|PB|的最小值.
),B是曲线ρ=﹣2sinθ上的动点,求|PA|+|PB|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网店经营的一种商品进价是每件10元,根据一周的销售数据得出周销量P(件)与单价x(元)之间的关系如图折线所示,该网店与这种商品有关的周开支均为25元.
(I)根据周销量图写出周销量P(件)与单价x(元)之间的函数关系式;
(Ⅱ)写出周利润y(元)与单价x(元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.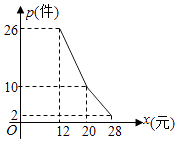
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为A、B、C的对边,且满足2(a2﹣b2)=2accosB+bc
(1)求A
(2)D为边BC上一点,CD=3BD,∠DAC=90°,求tanB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列函数中,满足“f(x+y)=f(x)f(y)”的单调递增函数是( )
A.f(x)=x3
B.f(x)=x ![]()
C.f(x)=3x
D.f(x)=( ![]() )x
)x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos(2x ![]() )﹣2sin(x
)﹣2sin(x ![]() )cos(x
)cos(x ![]() )
)
(1)求函数f(x)的最小正周期; (Ⅱ)求函数f(x)在区间[﹣ ![]() ,
, ![]() ]上的值域.
]上的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com