
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)讨论![]() 的单调性;
的单调性;
(Ⅱ)若![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)求导后,分![]() 、
、![]() 及
及![]() 三种情况讨论,分析导数
三种情况讨论,分析导数![]() 在区间
在区间![]() 上符号的变化,即可得出函数
上符号的变化,即可得出函数![]() 的单调区间;
的单调区间;
(Ⅱ)原命题等价于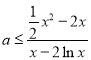 ,令函数
,令函数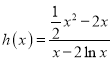 ,利用导数求出函数
,利用导数求出函数![]() 的最小值,即可得出实数
的最小值,即可得出实数![]() 的取值范围.
的取值范围.
(Ⅰ)![]() ,定义域为
,定义域为![]() ,且
,且![]() .
.
①当![]() 时,令
时,令![]() ,得
,得![]() .
.
若![]() ,
,![]() ;若
;若![]() ,
,![]() .
.
此时,函数![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ;
;
②当![]() 时,对任意的
时,对任意的![]() ,
,![]() ,
,
此时,函数![]() 的单调递减区间为
的单调递减区间为![]() ;
;
③当![]() 时,令
时,令![]() ,得
,得![]() .
.
若![]() ,
,![]() ;若
;若![]() ,
,![]() .
.
此时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
综上所述,当![]() 时,函数
时,函数![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ;
;
当![]() 时,函数
时,函数![]() 的单调递减区间为
的单调递减区间为![]() ;
;
当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
(Ⅱ)由![]() 即为
即为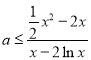 ,令
,令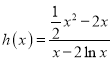 ,
,
则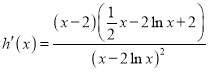 ,
,
令![]() ,则
,则![]() ,令
,令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
所以,函数![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() .
.
![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
所以,函数![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ,
,
所以,函数![]() 的最小值为
的最小值为![]() ,
,![]() .
.
因此,实数![]() 的取值范围是
的取值范围是![]() .
.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() ,g(x)=|xlnx﹣ax2|,a
,g(x)=|xlnx﹣ax2|,a![]() .
.
(1)讨论f(x)的单调性;
(2)若g(x)在区间(1,e)有极小值,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+blnx(a,b∈R)在点(1,f(1))处的切线方程为y![]() x﹣1.
x﹣1.
(1)求ab的值;
(2)当x>1时,f(x)![]() 0恒成立,求实数k的取值范围;
0恒成立,求实数k的取值范围;
(3)设g(x)=ex![]() x,求证:对于x∈(0,+∞),g(x)﹣f(x)>2恒成立.
x,求证:对于x∈(0,+∞),g(x)﹣f(x)>2恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在![]() 上的函数
上的函数![]() ,若存在正常数
,若存在正常数![]() 、
、![]() ,使得
,使得![]() 对一切
对一切![]() 均成立,则称
均成立,则称![]() 是“控制增长函数”,在以下四个函数中:①
是“控制增长函数”,在以下四个函数中:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .是“控制增长函数”的有( )
.是“控制增长函数”的有( )
A.②③B.③④C.②③④D.①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)若不等式![]() 对
对![]() 恒成立,求
恒成立,求![]() 的值;
的值;
(2)若![]() 在
在![]() 内有两个极值点,求负数
内有两个极值点,求负数![]() 的取值范围;
的取值范围;
(3)已知![]() ,
,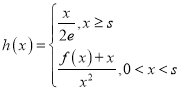 ,若对任意实数
,若对任意实数![]() ,总存在正实数
,总存在正实数![]() ,使得
,使得![]() 成立,求正实数
成立,求正实数![]() 的取值集合.
的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 是两条不同的直线,
是两条不同的直线,![]() ,
,![]() ,
,![]() 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若![]() ,
,![]() ,则
,则![]()
②若![]() ,
,![]() ,
,![]() ,则
,则![]()
③若![]() ,
,![]() ,则
,则![]()
④若![]() ,
,![]() ,则
,则![]()
其中正确命题的序号是( )
A.①和②B.②和③C.③和④D.①和④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生产旅游纪念品的工厂,拟在2017年度进行系列促销活动.经市场调查和测算,该纪念品的年销售量x(单位:万件)与年促销费用t(单位:万元)之间满足3-x与t+1成反比例.若不搞促销活动,纪念品的年销售量只有1万件.已知工厂2017年生产纪念品的固定投资为3万元,每生产1万件纪念品另外需要投资32万元.当工厂把每件纪念品的售价定为“年平均每件生产成本的1.5倍”与“年平均每件所占促销费的一半”之和时,则当年的产量和销量相等.(利润=收入-生产成本-促销费用)
(1)请把该工厂2017年的年利润y(单位:万元)表示成促销费t(单位:万元)的函数;
(2)试问:当2017年的促销费投入多少万元时,该工厂的年利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com